리셉턴스 합성 기법을 이용한 공작기계 모듈러 설계 방법론 연구

1. 서 론

공작기계는 ‘mother of machines’라고 불리며, 제조업 분야에서 기계 부품을 만드는 정밀기계로서 핵심적인 역할을 수행한다. 공작기계의 공구선단에서 발생하는 진동은 공작물의 가공 품질에 직접적인 영향을 미치기 때문에, 이를 선행적으로 예측하는 것이 제품 개발에서 중요한 이슈이다. 따라서 가상 제품 개발 단계에서 공작기계의 공구선단에서 발생하는 진동으로부터 채터 안정 선도를 도시하여 공구와 공작물 사이의 상대 진동으로 발생하는 채터진동을 회피할 수 있고, 안정적인 가공과 표면 품위 향상을 도모할 수 있다. 공작기계의 공구선단에서 진동을 예측하는 receptance coupling substructure analysis(RCSA) 기법은 단품의 리셉턴스를 합성해 결합품의 동특성을 예측하는 동적 부구조법 중 하나이다. RCSA 기법을 이용해 원하는 성능에 도달하기 위한 설계변수를 최적화하는 모듈러 설계 기법에 적용할 수 있다. 모듈러 설계 기법은 공차, 재질, 치수 등 다양한 설계 변경을 적용한 단품을 결합하여 결합품의 성능을 예측 및 평가하는 기법으로 설계의 유연성을 제공한다.

Schmitz et al.은 RCSA 기법을 이용해 공작기계의 공구와 공구 홀더의 리셉턴스를 합성해 공구선단에서 동특성을 예측하였다⁽¹⁾. Ito et al.은 공작기계 설계에 적용되는 다양한 모듈러 설계 방법을 제시하였다⁽²⁾. Cao et al.은 해석 모델의 결합 조건을 이용해 베어링 모델링 기법을 제시하였다⁽³⁾.

이 연구에서는 공작기계 해석 모델을 대상으로 공구와 공구 홀더뿐만 아니라 커플러, 락너트 등 주요 설계변수에 RCSA 기법을 적용해, 공구선단에서 동특성을 예측하고 전체 해석 시간을 가속화하는 모듈러 설계 방법론을 제시하였다. 이를 위해 첫 번째로, RCSA 수식을 이용하여 유한요소 해석에 사용되는 결합 조건을 구현하였다. 다음으로, 주파수응답함수를 계산하는 기존의 해석 방식을 개선하고 연산 최적화를 통해 정확도를 향상시켰다. 마지막으로, 자유도 축소를 통해 연산 시간을 단축시켰다. 이를 통해 설계 변경시 발생하는 다양한 결합품의 동특성을 기존 대비 5배 이상 빠르게 예측 가능함을 확인하였다.

2. 배경 이론

2.1 다중 점 구속

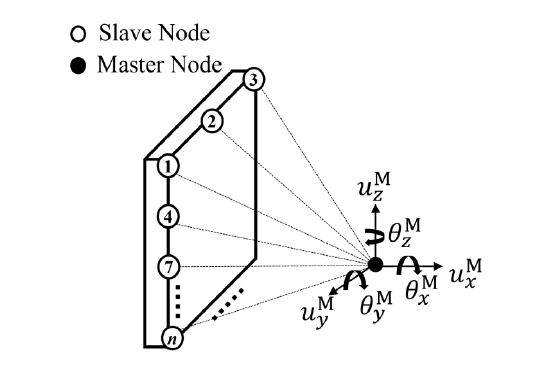
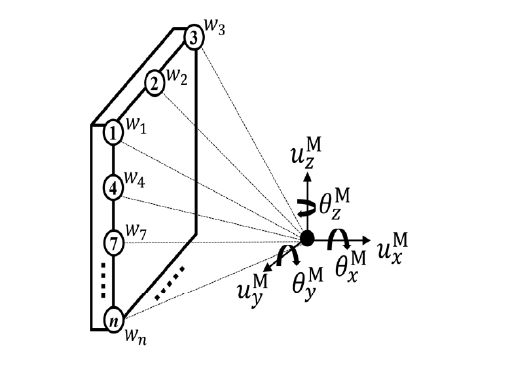
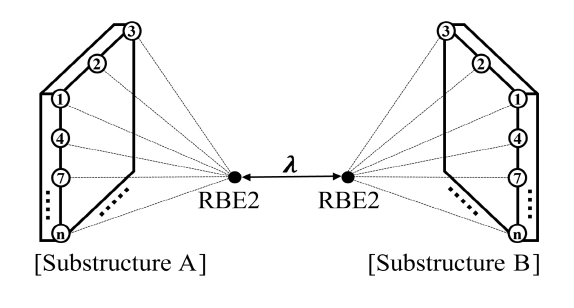
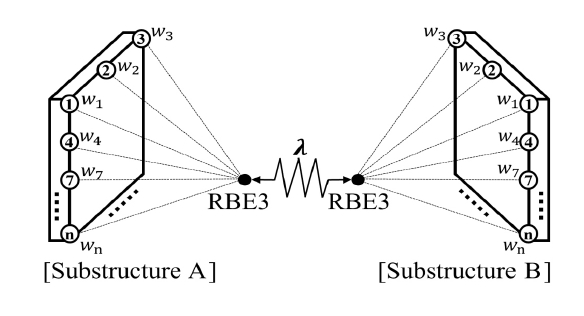
다중 점 구속은 여러 개의 노드에 특정한 구속 조건을 주는 방식이며 대표적으로 rigid body element (RBE)를 이용한 결합이 있다. 다중 점 구속을 사용하면, 단품과 단품이 연결되는 결합면에 존재하는 슬레이브 노드를 한 개의 6 자유도 마스터 노드로 단순화시켜 모델링할 수 있다. RBE2는 Fig. 1과 같이 강체 요소로 표현되며, 결합면의 슬레이브 노드를 그룹화 시켜 한개의 마스터 노드로 표현한다. 이 때 마스터 노드의 응답은 슬레이브 노드의 응답에 독립적인 특성을 가진다. 따라서, 마스터 노드의 응답만을 이용해 강체 결합면으로 모델링할 수 있다. RBE3은 Fig. 2와 같이 보간 요소로 표현되며, 결합면의 슬레이브 노드를 그룹화 시켜 한개의 마스터 노드로 표현한다. 이 때 마스터 노드의 응답은 슬레이브 노드의 응답을 이용해 계산되며, 결합면의 강성은 각 슬레이브 노드의 가중치를 통해 표현될 수 있다. 따라서 마스터 노드의 변위는 슬레이브 노드의 변위에 의해 결정되며⁽⁴⁾, 강성을 가지는 결합면으로 모델링 될 수 있다. 이 때 마스터 노드의 응답인 병진 변위 u^M와 회전 변위 θ^M는 n개의 슬레이브 노드의 응답인 병진 변위 u^S로 나타낼 수 있으며, 식 (1) ~ 식 (2)로 계산된다^(5,6). 이 때 3 자유도 슬레이브 노드가 6 자유도 마스터 노드의 변위를 표현할 수 있도록 n을 3 이상으로 하여, 미지수보다 방정식이 많은 과결정 연립방정식의 해를 계산한다.

Fig. 1

Rigid interface coupling using RBE2

Fig. 2

Flexible interface coupling using RBE3

$\[ {\mathbf{u}}^{\mathrm{M}}=\frac{\sum _{k=1}^n{w}_k{\mathbf{u}}_k^{\mathrm{S}}}{\sum _{k=1}^n{w}_k} \]$

(1)

$\[ {\mathbf{\theta }}^{\mathbf{M}}=\frac{\sum _{k=1}^n{w}_k\left({\mathbf{r}}_k\times {\mathbf{u}}_k^{\mathrm{S}}\right)}{\sum _{k=1}^n{w}_k\left|{\mathbf{r}}_k\right|\left|{\mathbf{r}}_k\right|} \]$

(2)

2.2 Tie 결합

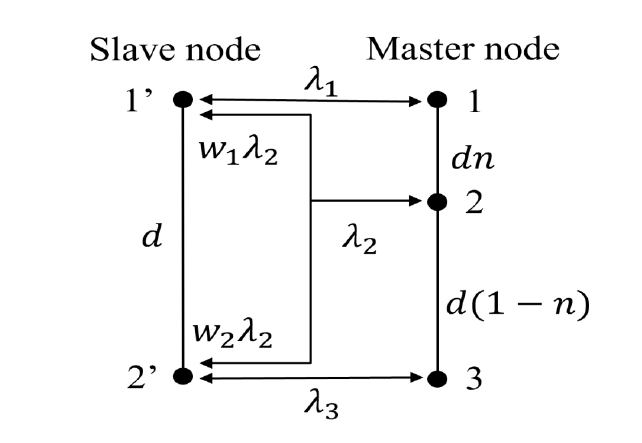
Tie는 접촉 요소로 표현되며, 접촉 영역이 접합되면 면 또는 선 사이에서 슬라이딩과 분리가 허용되지 않는 결합이다. Tie 결합은 Fig. 3과 같이 결합면의 모든 슬레이브 노드와 마스터 노드는 일대일 또는 일대다로 결합되며⁽⁷⁾, 식 (3) ~ 식 (4)로 변위 호환성과 힘의 평형식을 만족시킨다.

Fig. 3

Node coupling using Tie

$\[ {\lambda }_2=w_1{\lambda }_2+w_2{\lambda }_2 \]$

(3)

$\[ \left(dn\right)w_1{\lambda }_2-d\left(1-n\right)w_2{\lambda }_2=0 \]$

(4)

2.3 RCSA 이론

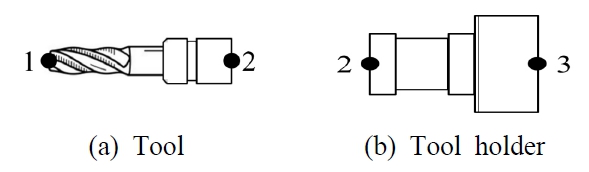
리셉턴스는 시스템의 동특성을 나타내는 물리량으로, 시스템에 단위 힘이 가해졌을 때의 변위를 주파수 영역에서 나타내는 주파수응답함수이다. RCSA는 단품의 리셉턴스만을 이용해 결합품의 리셉턴스를 예측하는 기법이다. RCSA 기법을 적용하기 위해 각 단품이 연결되는 노드에서 변위 호환성과 힘의 평형식을 만족시켜야 하며 식 (5)로 Fig. 4의 결합품 AB에 대한 주파수응답함수를 계산할 수 있다⁽⁸⁾.

Fig. 4

Substructure

$\[ \begin{array}{ll}{\mathbf{H}}^{\mathrm{A}\mathrm{B}}& =\left[\begin{array}{c}{\mathbf{H}}_{11}^{\mathrm{A}\mathrm{B}}{\mathbf{H}}_{13}^{\mathrm{A}\mathrm{B}}\\ {\mathbf{H}}_{31}^{\mathrm{A}\mathrm{B}}{\mathbf{H}}_{33}^{\mathrm{A}\mathrm{B}}\end{array}\right]\\ & =\left[\begin{array}{cc}{\mathbf{H}}_{11}^{\mathrm{A}}-{\mathbf{H}}_{12}^{\mathrm{A}}{\left({\mathbf{H}}_{\mathrm{J}}\right)}^{-1}{\mathbf{H}}_{21}^{\mathrm{A}}& {\mathbf{H}}_{12}^{\mathrm{A}}{\left({\mathbf{H}}_{\mathrm{J}}\right)}^{-1}{\mathbf{H}}_{23}^{\mathrm{B}}\\ {\mathbf{H}}_{32}^{\mathrm{B}}{\left({\mathbf{H}}_{\mathrm{J}}\right)}^{-1}{\mathbf{H}}_{21}^{\mathrm{A}}& {\mathbf{H}}_{33}^{\mathrm{B}}-{\mathbf{H}}_{32}^{\mathrm{B}}{\left({\mathbf{H}}_{\mathrm{J}}\right)}^{-1}{\mathbf{H}}_{23}^{\mathrm{B}}\end{array}\right]\end{array} \]$

(5)

$\[ {\mathbf{H}}_{\mathrm{J}}={\mathbf{H}}_{22}^{\mathrm{A}}+{\mathbf{H}}_{22}^{\mathrm{B}}+{\mathbf{K}}^{-1} \]$

(6)

식 (5)와 식 (6)을 바탕으로 단품 A, B의 주파수응답함수를 이용해 결합품 AB의 주파수응답함수를 예측할 수 있다.

3. 모듈러 설계 적용

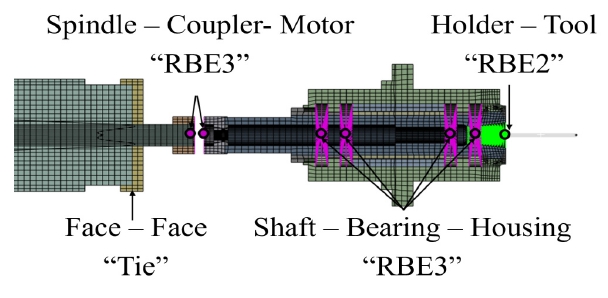
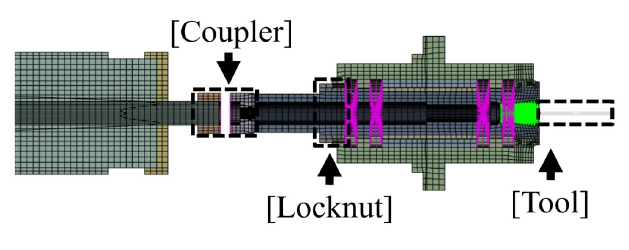
5축 수직 머시닝 센터의 직 체결 구동 스핀들이 대상 모델로 사용됐다. 대상 모델은 22개의 단품으로 구성돼 있으며, Fig. 5와 같이 RBE2, RBE3, Tie 결합이 사용됐다. Intel^® Core^™ i9-12900 3.20 GHz, 64 GB RAM 사양의 PC를 사용하였고, ABAQUS CAE에서 란초스 알고리즘(Lanczos method)을 적용해 모드 해석을 수행하였다.

Fig. 5

Machine tool FEA model

3.1 연산 최적화

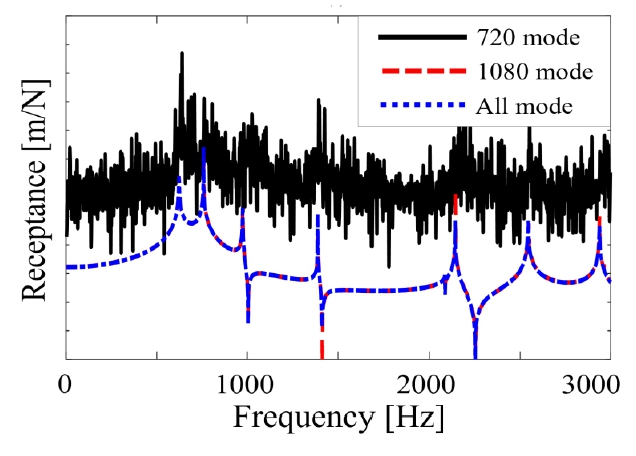
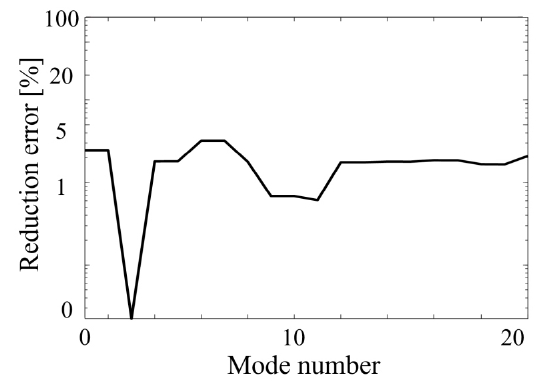
초기에는 모드 중첩법을 사용할 때, RCSA 오차가 발생하지 않는 최적의 모드 개수를 결정하는 연구가 수행됐다. 예를 들어, 240개 노드의 주파수응답함수를 합성하기 위해 필요한 최소 구속 조건의 수는 노드 개수에 병진 자유도 3을 곱한 720개다. 하지만 Fig. 6과 같이 필요한 모드 개수가 단품의 기하학적 특성에 따라 서로 다른 경향성을 보이기 때문에, 모드 개수를 최대로 사용하고 연산 속도를 최적화하는 방향으로 접근했으며, 특이값 분해 이론을 응용했다. 특이값 분해는 행렬을 U, Σ, V 세 개의 행렬로 분해하는 기법이다. 여기서 Σ는 행렬의 특이 값을 대각선에 배열한 대각 행렬이다. 대각 행렬을 곱하는 것은 M개의 곱셈을 1개의 병렬연산으로 만들어, 연산 시간을 단축시킬 수 있다. 때문에 식 (17)과 같이 모드 중첩법을 특이값 분해와 유사한 형식으로 분해하였다.

Fig. 6

Difference in RCSA result due to number of modes

$\[ \mathbf{H}=\sum _{i=1}^M\frac{{\left\{{\mathbf{\varphi }}_i\right\}}^{\mathrm{T}}\left\{{\mathbf{\varphi }}_i\right\}}{\left({\omega }_i^2-{\omega }^2\right)+j2{\omega }_i\omega {\zeta }_i}=\mathbf{U}\sum {\mathbf{V}}^{\mathrm{T}} \]$

(17)

이를 통해 모드 개수가 계산 시간에 미치는 영향을 최소화하고, 모드 중첩법을 적용할 때 주파수응답함수의 정확도를 최대한으로 향상시킬 수 있다.

3.2 RCSA 수식을 이용한 결합 구현

(1) RBE를 이용한 결합 구현

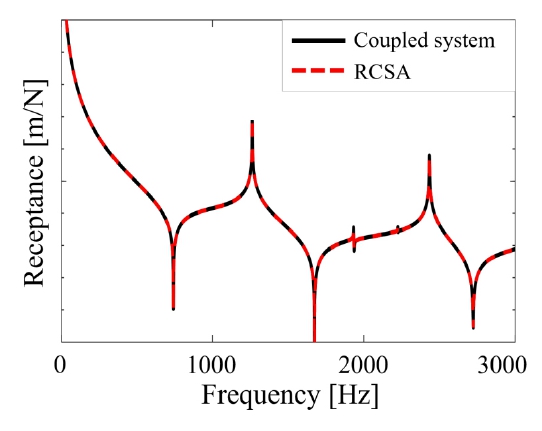
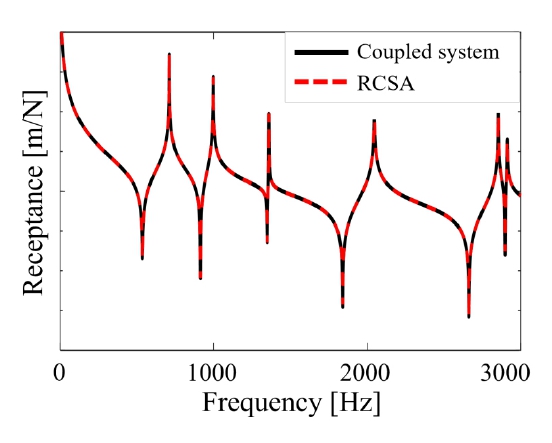
RBE2는 Fig. 7과 같이 마스터 노드의 응답이 슬레이브 노드의 응답에 독립적이고, 한 개의 마스터 노드 변위를 측정함으로써 강체 결합면의 변위를 계산할 수 있다. RBE3은 Fig. 8과 같이 마스터 노드의 응답이 슬레이브 노드의 응답으로 계산되며, 한 개의 마스터 노드 변위를 측정해 강성을 가진 결합면의 변위를 계산할 수 있다. 대상 모델은 RBE2를 이용해 공구와 홀더를 결합했다. 베어링 또는 커플러는 RBE3을 이용해 결합됐으며, 연결부 강성 행렬에 정강성 값을 대입하였다.

Fig. 7

RBE2 configuration

Fig. 8

RBE3 configuration

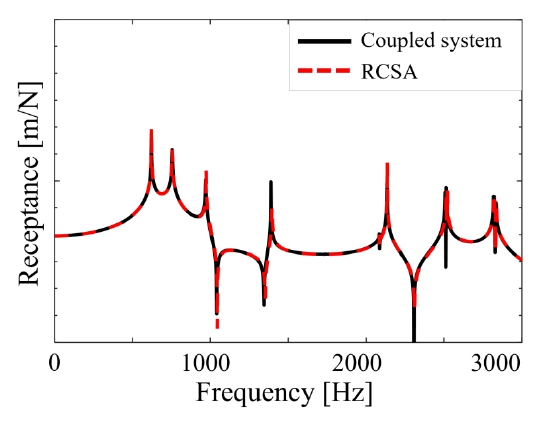
Fig. 9와 Fig. 10과 같이 RCSA 기법이 높은 정확도를 나타내는 것을 확인할 수 있다. 결과적으로 RBE 결합을 RCSA 수식을 이용해 구현했다.

Fig. 9

RCSA result using RBE2

Fig. 10

RCSA result using RBE3

(2) Tie 결합 구현

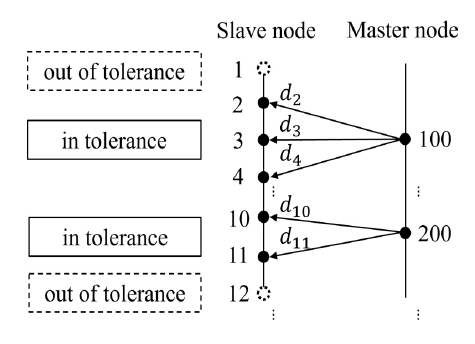
RCSA 기법을 이용해 Tie 결합을 구현하기 위해선 각 단품의 결합면에 있는 모든 노드의 주파수응답함수를 합성해야 한다. 이 때 결합면의 슬레이브 노드는 일정 허용 범위 내에 있는 마스터 노드에만 결합된다. 이를 구현하기 위해 마스터 노드의 허용 범위 내에 있는 슬레이브 노드의 거리와 노드 번호를 행렬로 구성하였다. 이를 통해 노드의 주파수응답함수가 합성될 때 새로운 변위 호환성과 힘의 평형식을 식 (18) ~ 식 (21)과 같이 표현할 수 있다.

$\[ w_2{u}_2^{\mathrm{S}}+w_3{u}_3^{\mathrm{S}}+w_4{u}_4^{\mathrm{S}}=u_{100}^{\mathrm{M}} \]$

(18)

$\[ w_2{\lambda }_{100}+w_3{\lambda }_{100}+w_4{\lambda }_{100}={\lambda }_{100} \]$

(19)

$\[ w_{10}{u}_{10}^{\mathrm{S}}+w_{11}{u}_{11}^{\mathrm{S}}=u_{200}^{\mathrm{M}} \]$

(20)

$\[ w_{10}{\lambda }_{200}+w_{11}{\lambda }_{200}={\lambda }_{200} \]$

(21)

여기서 변위 u와 라그랑주 승수 λ에 곱해지는 가중치 w는 마스터 노드의 허용범위 내에 있는 슬레이브 노드의 거리 비율로 식 (22)와 식 (23)과 같이 나타낼 수 있다.

$\[ w_2=\frac{d_2}{d_2+d_3+d_4} \]$

(22)

$\[ w_{10}=\frac{d_{10}}{d_{10}+d_{11}} \]$

(23)

이를 통해 새로운 구속 조건을 만족하는 가중치 이진 행렬 B_W를 구성할 수 있으며, Fig. 11과 같이 Tie 결합을 구현할 수 있는 RCSA 식 (24)와 식 (25)를 유도할 수 있다.

Fig. 11

Tie configuration

$\[ {\mathbf{B}}_{\mathrm{w}}\mathbf{u}=0 \]$

(24)

$\[ {\mathbf{H}}_{\mathrm{T}\mathrm{i}\mathrm{e}\mathrm{ }}^{\mathrm{A}\mathrm{B}}=\mathbf{H}-{\mathbf{H}\mathbf{B}}_{\mathrm{w}}^{\mathrm{T}}{\left({\mathbf{B}}_{\mathrm{w}}{\mathbf{H}\mathbf{B}}_{\mathrm{w}}^{\mathrm{T}}\right)}^{-1}{\mathbf{B}}_{\mathrm{w}}\mathbf{H} \]$

(25)

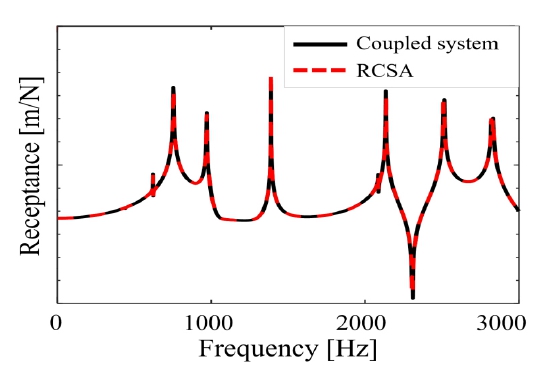
이를 통해 결합면이 960개의 슬레이브 노드로 구성된 락너트와 480개의 마스터 노드로 구성된 스핀들을 결합했고, 결과는 Fig. 12와 같다.

Fig. 12

RCSA result using Tie

3.3 자유도 축소

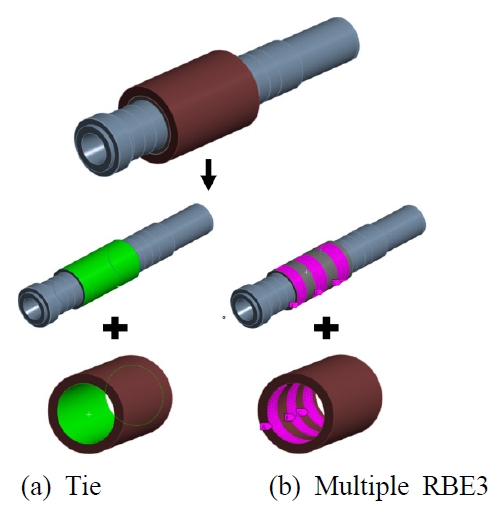
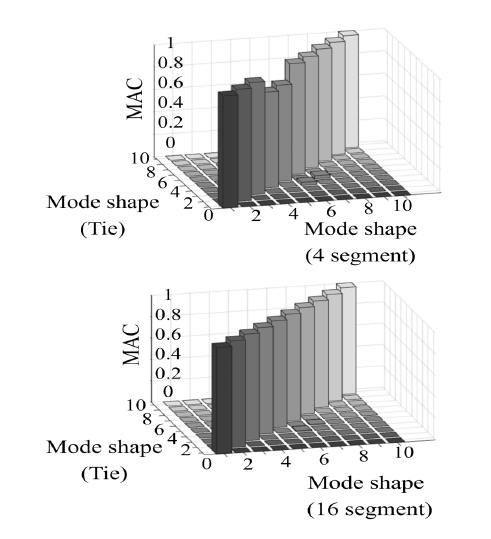
결합 노드의 개수가 증가하면, 주파수응답함수 행렬 H의 크기가 커져 역행렬 연산 시간이 증가한다. 따라서 이를 감소시키기 위해 결합면 노드의 자유도를 축소시켜 행렬의 크기를 줄여야 할 필요성이 존재한다. 때문에 Fig. 13과 같이 내륜 베어링 스페이서와 Tie 결합된 외륜 베어링 스페이서의 결합 영역을 여러 개의 RBE3으로 나누어 자유도를 축소시키는 방법으로 접근했으며, 이를 검증하기 위해 식 (26)을 이용해 Tie 결합 모델과 자유도 축소 모델의 모드상관계수(MAC: modal assurance criterion)⁽¹¹⁾를 계산하였다.

Fig. 13

Multiple segments using RBE3

Fig. 14와 같이 타겟 주파수인 3000 Hz까지 나타나는 모드 10개에 대한 모드상관계수를 계산했으며 RBE3으로 나누는 개수가 증가함에 따라 모드상관계수가 1에 가까워지는 것을 확인하며 자유도 축소의 타당성을 검증했고, 식 (27)을 이용해 모드 형상 벡터의 자유도를 감소시켰다⁽¹²⁾. 이 때 +는 무어 펜로즈의 의사역행렬(Moore-Penrose pseudo inverse matrix) 연산을 의미한다.

Fig. 14

MAC difference according to number of RBE3 segment

$\[ \frac{{\left|{\left\{{\mathbf{\varphi }}_{\mathrm{T}\mathrm{i}\mathrm{e}\mathrm{ }}\right\}}^{\mathrm{T}}\left\{{\mathbf{\varphi }}_{\mathrm{r}\mathrm{e}\mathrm{d}\mathrm{u}\mathrm{c}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n}}\right\}\right|}^2}{\left({\left\{{\mathbf{\varphi }}_{\mathrm{T}\mathrm{i}\mathrm{e}}\right\}}^{\mathrm{T}}\left\{{\mathbf{\varphi }}_{\mathrm{T}\mathrm{i}\mathrm{e}}\right\}\right)\left({\left\{{\mathbf{\varphi }}_{\mathrm{r}\mathrm{e}\mathrm{d}\mathrm{u}\mathrm{c}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n}}\right\}}^{\mathrm{T}}\left\{{\mathbf{\varphi }}_{\mathrm{r}\mathrm{e}\mathrm{d}\mathrm{u}\mathrm{c}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n}}\right\}\right)} \]$

(26)

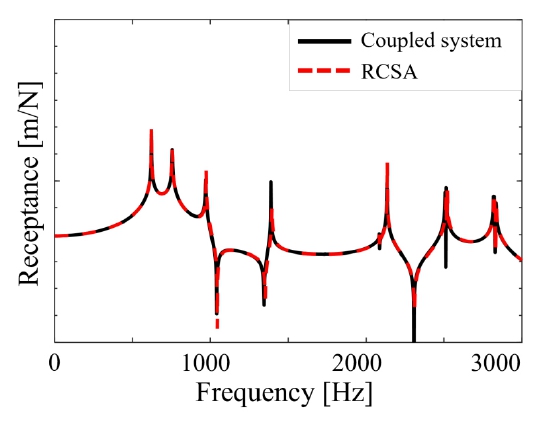
식 (28)은 n개의 3자유도 슬레이브 노드를 1개의 6자유도 마스터 노드로 자유도를 축소하는 행렬이다. 식 (29)는 자유도 축소 이전 n개의 3자유도 슬레이브 노드 응답을 나타내는 열 벡터이며, 식 (30)은 자유도가 축소된 1개의 6자유도 마스터 노드 응답을 나타내는 열 벡터이다. 이 때 RBE3으로 나누는 개수는 모드 중첩법으로 발생하는 오차와 자유도 축소로 발생하는 오차가 최소가 되도록 선정했고, 이는 노드에 구속 조건이 중복되지 않고 한 번만 적용될 때이다. 이를 통해 결합면의 1020개 노드를 90개의 RBE3으로 축소시켰고 기존 모델과 축소된 모델을 비교해 계산되는 reduction error를 식 (31)를 이용해 계산해 4 % 이내로 예측하였으며 결과는 Fig. 15와 Fig. 16과 같다. 또한 주파수응답함수의 응답을 비교하는 유사도를 식 (32)를 이용해 계산하였고 결과는 Fig. 17과 같다. 최종적으로 Tie 결합을 이용해 RCSA를 적용할 때와 비교했을 때 주파수응답함수를 21배 빠르게 계산할 수 있다.

Fig. 15

Calculated reduction error

Fig. 16

RCSA result using reduction

Fig. 17

Similarity results using reduction

$\[ {\mathbf{R}}^{+}{\mathbf{\varphi }}_n={\mathbf{\varphi }}_n^{\mathrm{r}\mathrm{e}\mathrm{d}\mathrm{u}\mathrm{c}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n}\mathrm{ }} \]$

(27)

$\[ {\mathbf{R}}^{+}={\left[\begin{array}{cc}\begin{array}{ccc}1& 0& 0\\ 0& 1& 0\\ 0& 0& 1\end{array}& \begin{array}{ccc}0& r_{1,z}& -r_{1,y}\\ -r_{1,z}& 0& r_{1,x}\\ r_{1,y}& -r_{1,x}& 0\end{array}\\ & ⋮\\ \begin{array}{ccc}1& 0& 0\\ 0& 1& 0\\ 0& 0& 1\end{array}& \begin{array}{ccc}0& r_{n,z}& -r_{n,y}\\ -r_{n,z}& 0& r_{n,x}\\ r_{n,y}& -r_{n,x}& 0\end{array}\end{array}\right]}_{6\times 3n}^{+} \]$

(28)

$\[ {\mathbf{\varphi }}_n={\left[\begin{array}{c}{u}_{1,x}^S\\ u_{1,y}^S\\ u_{1,z}^S\\ ⋮\\ u_{n,x}^S\\ u_{n,y}^S\\ u_{n,z}^S\end{array}\right]}_{3n\times 1} \]$

(29)

$\[ {\mathbf{\varphi }}_n^{\mathrm{r}\mathrm{e}\mathrm{d}\mathrm{u}\mathrm{c}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n} }={\left[\begin{array}{c}{u}_{1,x}^{\mathrm{M}}\\ u_{1,y}^{\mathrm{M}}\\ u_{1,z}^{\mathrm{M}}\\ {\theta }_{1,x}^{\mathrm{M}}\\ {\theta }_{1,y}^{\mathrm{M}}\\ {\theta }_{1,z}^{\mathrm{M}}\end{array}\right]}_{6\times 1} \]$

(30)

$\[ \mathrm{R}\mathrm{e}\mathrm{d}\mathrm{u}\mathrm{c}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n}\mathrm{ }\mathrm{e}\mathrm{r}\mathrm{r}\mathrm{o}\mathrm{r}\mathrm{ }=\frac{\mathrm{norm}\left(\left({\mathbf{R}\mathbf{R}}^{+}-\mathbf{I}\right)\mathbf{\varphi }\right)}{\mathrm{n}\mathrm{o}\mathrm{r}\mathrm{m}\left(\mathbf{\varphi }\right)}\times 100 \]$

(31)

$\[ \mathrm{S}\mathrm{i}\mathrm{m}\mathrm{i}\mathrm{l}\mathrm{a}\mathrm{r}\mathrm{i}\mathrm{t}\mathrm{y}\mathrm{ }=\frac{\left|{\mathbf{H}}^{\mathrm{A}}\left(\omega \right)-{\mathbf{H}}^{\mathrm{B}}\left(\omega \right)\right|}{\mathrm{m}\mathrm{a}\mathrm{x}\left(\left|{\mathbf{H}}^{\mathrm{A}}\left(\omega \right)\right|,\left|{\mathbf{H}}^{\mathrm{B}}\left(\omega \right)\right|\right)}\times 100 \]$

(32)

4. 결 과

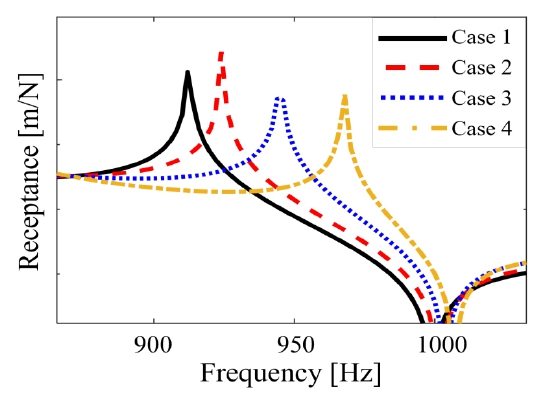
설계 변경이 필요한 단품의 동특성을 나타내는 주파수응답함수 행렬 H를 구성하고 RCSA 수식을 통한 결합 조건 적용 및 자유도 축소를 통해, 기존의 해석 프로세스보다 5배 이상 빠르게 결과를 예측할 수 있다. Fig. 18과 같이 설계 변경 대상품을 선정하여, 필요한 경우의 수를 Table 1로 만들고, 모드 중첩법을 이용해 단품의 주파수응답함수를 계산해 모듈러 설계 방법론을 적용하면, 결합품의 동특성을 예측하는 연산 시간을 단축시킬 수 있는 것을 확인하였다. 여기서 RBE2, RBE3, Tie 결합이 모두 사용됐으며, 락너트에 대해 자유도 축소가 적용됐다. 이를 통해 첫 번째 구조물에는 a개, 두 번째 구조물에는 b개, 세번째 구조물에는 c개의 설계 변경에 대한 경우의 수가 있을 때, a × b × c개 결합품에 대한 해석 모델을 만들고 주파수응답함수를 계산하는 대신, a + b + c개 단품에 대한 주파수응답함수를 이용해, a × b × c개 결합품의 주파수응답함수를 예측하고, Fig. 19와 같이 원하는 주파수 대역에서 필요한 설계 변수를 최적화할 수 있다.

Fig. 18

Target substuructure for design change

Table 1

Modular design change of machine tool

Fig. 19

Results using RCSA methodology

5. 결 론

이 연구에서 공작기계 해석 모델에 대한 모듈러 설계 방법론을 제시하였으며, 결과적으로 단품의 주파수응답함수를 이용해 기존 해석 프로세스보다 5배 이상 빠르게 결합품의 주파수응답함수를 예측하는 프로세스를 개발했다. 이를 위해 첫 번째로 모드 중첩법을 이용해 연산 기법 최적화를 수행하였다. 두 번째로 단품과 단품을 결합하는 RBE2, RBE3, Tie 결합을 RCSA 수식을 이용해 적용 가능하도록 만들었다. RBE 결합은 마스터 노드의 주파수응답함수만을 합성하지만, Tie 결합은 결합면에 존재하는 모든 노드의 주파수응답함수를 합성해야 하므로 연산 시간이 길어지는 단점이 있다. 때문에 세 번째로 결합면의 자유도를 축소시켜 역행렬 연산 시간을 단축시켰고, reduction error 4 % 이내로 주파수응답함수를 예측했다.

가상 제품 개발 단계에서는 원가, 무게 등의 다양한 요인을 고려한 설계 변수 최적화가 필요하며, 개발 초기 단계에 시스템 단위로 다양한 설계 변수를 검토해야 한다. 이 때 설계 변수가 늘어날수록 계산할 주파수응답함수의 개수가 증가하기 때문에, 모든 경우에 대하여 경계조건을 모델링하고 결합품을 만들어 주파수응답함수를 계산하는 것은 현실적으로 어려움이 있다. 해당 기법은 모든 설계 변수에 대한 주파수응답함수를 데이터 베이스로 구축하고 경향성 분석이 가능하다는 것에 강점을 가지고 있다.

최근 인공 지능과 디지털 트윈 기술의 발전으로 제조업은 다품종 소량생산 추세로 변화하고 있다. 이에 따라 가상 제품 개발 단계에서 정밀도가 낮은 모델을 사용해 computer aid engineering(CAE)를 수행하고, 이 결과를 바탕으로 설계 방향을 결정해 다양한 설계에 대응하는 패러다임이 등장하기 시작했다⁽¹³⁾. 이 연구에서 제안된 모듈러 설계 기법은 가상 제품 개발 단계에서 설계 변수를 최적화하고 설계 방향을 설정하는 데 활용될 수 있을 것으로 기대된다. 향후에는 시험과 해석 융합을 통해 하이브리드 모델을 구축하고^(14~16), 결합면의 강성 및 감쇠 행렬 규명^(17~19)을 통해 실험 RCSA의 정확도를 향상시켜 실험 단계에서 모듈러 설계를 적용하는 연구를 수행하는 것을 목표로 하고 있다.

Acknowledgments

이 연구는 (주) DN솔루션즈, 서울대학교 공학연구원, 교육부 및 한국연구재단의 4단계 두뇌한국21 사업(4단계 BK21 사업)의 지원을 통해 진행되었으며, 2023년 추계 소음진동공학회에서 발표한 내용을 토대로 작성되었다.

References

• Schmitz, T. L. and Duncan, G. S., 2005, Three-component Receptance Coupling Substructure Analysis for Tool Point Dynamics Prediction, Journal of Manufacturing Science and Engineering, Vol. 127, No. 4, pp. 781~790. [https://doi.org/10.1115/1.2039102]
• Ito, Y., 2008, Modular Design for Machine Tools, McGraw-hill Education, 1st Edition, NY, United States.
• Cao, H., Li, Y. and Chen, X., 2016, A New Dynamic Model of Ball-bearing Rotor Systems based on Rigid Body Element, Journal of Manufacturing Science and Engineering, Vol. 138, No. 7, 071007. [https://doi.org/10.1115/1.4032582]
• Brecher, C., Fey, M., Tenbrock, C. and Daniels, M., 2016, Multipoint Constraints for Modeling of Machine Tool Dynamics, Journal of Manufacturing Science and Engineering, Vol. 138, No. 5, 051006. [https://doi.org/10.1115/1.4031771]
• Heirman, G. H. K. and Desmet, W., 2010, Interface Reduction of Flexible Bodies for Efficient Modeling of Body Flexibility in Multibody Dynamics, Multibody System Dynamics, Vol. 24, pp. 219~234. [https://doi.org/10.1007/s11044-010-9198-7]
• Ahn, J.-G., Yang, H.-I. and Kim, J.-G., 2020, Multipoint Constraints with Lagrange Multiplier for System Dynamics and Its Reduced-order Modeling, AIAA Journal, Vol. 58, No. 1, pp. 385~401. [https://doi.org/10.2514/1.J058118]
• Mokotoff, P. and Dannenhoffer, J., 2022, Exploring Tie Constraints for Structural Analysis Problems, Proceedings of AIAA SCITECH Forum. [https://doi.org/10.2514/6.2022-0387]
• Tsai, J.-S. and Chou, Y.-F., 1988, The Identification of Dynamic Characteristics of a Single Bolt Joint, Journal of Sound and Vibration, Vol. 125, No. 3, pp. 487~502. [https://doi.org/10.1016/0022-460X(88)90256-8]
• De Klerk, D., Rixen, D. J. and Voormeeren, S. N., 2008, General Framework for Dynamic Substructuring: History, Review and Classification of Techniques, AIAA Journal, Vol. 46, No. 5, pp. 1169-1181. [https://doi.org/10.2514/1.33274]
• Cuppens, K., Sas, P. and Hermans, L., 2001, Evaluation of the FRF based Substructuring and Modal Synthesis Technique Applied to Vehicle FE Data, Proceedings of the International Seminar on Modal Analysis, Vol. 3, pp. 1143~1150.
• Allemang, R. J., 2003, The Modal Assurance Criterion - Twenty Years of Use and Abuse, Sound and Vibration, Vol. 37, No. 8, pp. 14~21.
• Van der Seijs, M. V., Van den Bosch, D. D., Rixen, D. J. and de Klerk, D., 2013, An Improved Methodology for the Virtual Point Transformation of Measured Frequency Response Functions in Dynamic Substructuring, Proceedings of 4th ECCOMAS Thematic Conference on Computational Methods in Structural Dynamics and Earthquake Engineering, Vol. 4, pp. 4334~4347.
• Solmaz, S., Kester, L. and Van Gerven, T., 2023, An Immersive Virtual Reality Learning Environment with CFD Simulation: Unveiling the Virtual Garage Concept, Education and Information Technologies, Vol. 29, pp. 1455~1488. [https://doi.org/10.1007/s10639-023-11747-z]
• Albertelli, P., Goletti, M. and Monno, M., 2013, A New Receptance Coupling Substructure Analysis Methodology to Improve Chatter Free Cutting Conditions Prediction, International Journal of Machine Tools and Manufacture, Vol. 72, pp.16~24. [https://doi.org/10.1016/j.ijmachtools.2013.05.003]
• Kang, S., Yang, S., Kim, S. J., Ju, H. J. and Kang, Y. J., 2020, Engine Mount Response Improvement using Hybrid Modeling and Bayesian Optimization, Transactions of the Korean Society for Noise and Vibration Engineering, Vol. 30, No. 6, pp. 546~552. [https://doi.org/10.5050/KSNVE.2020.30.6.546]
• Klaassen, S. W. B., Van der Seijs, M. V. and De Klerk, D., 2018, System Equivalent Model Mixing, Mechanical Systems and Signal Processing, Vol. 105, pp. 90~112. [https://doi.org/10.1016/j.ymssp.2017.12.003]
• Kim, J. G., Nam, K.-U. and Kang, Y. J., 2020, Method to Estimate Rotational Stiffness: Trial Masses, Virtual Masses, and Virtual Springs, Journal of Sound and Vibration, Vol. 477, 115321. [https://doi.org/10.1016/j.jsv.2020.115321]
• Özşahin, O., Budak, E. and Özgüven, H. N., 2015, Identification of Bearing Dynamics under Operational Conditions for Chatter Stability Prediction in High Speed Machining Operations, Precision Engineering, Vol. 42, pp. 53~65. [https://doi.org/10.1016/j.precisioneng.2015.03.010]
• Kono, D., Nishio, S., Yamaji, I. and Matsubara, A., 2015, A Method for Stiffness Tuning of Machine Tool Supports Considering Contact Stiffness, International Journal of Machine Tools and Manufacture, Vol. 90, pp. 50~59. [https://doi.org/10.1016/j.ijmachtools.2015.01.001]