진동내구 프로파일 도출을 통한 구동계 신뢰성 향상 기법
© The Korean Society for Noise and Vibration Engineering
Abstract
This paper presents a method for generating an accelerated vibration driving profile to evaluate the vibration durability of an automotive powertrain system. A key challenge in vibration durability testing is developing a vibration profile in a laboratory environment that accurately reproduces the vibration damage severity and characteristics observed under real-world conditions, taking into account the harsh operating environment of the vehicle. The optimal mounting positions for accelerometers on the target components are determined by analyzing the vibration transfer functions at candidate positions for 3-axis vibration measurements, each corresponding to a different channel. The optimal combination of road profiles was identified by comparing on-road data with special road data and analyzing sensitivity, pattern similarity, and correlations for each vibration channel. Furthermore, an optimization algorithm was applied to minimize errors in fatigue damage estimation and reduce the test duration, leading to the derivation of an optimal accelerated durability test mode. Through a comparative analysis of on-road data and special road data with iterative control to minimize errors, the vibration durability severity error rate was maintained within acceptable limits.
Keywords:
Vibration Durability, Power Spectral Density, Optimal Mounting Position, Powertrain, Multi-Axial Simulation Table키워드:
진동내구, 파워 스펙트랄 밀도, 마운팅 최적 위치, 파워트레인, 다축 시뮬레이션 테이블1. 서 론
일반적으로 차량은 약 1만개 이상의 다양한 부품으로 조합된 자유도가 높은 시스템이다. 따라서, 각각의 부품 및 시스템은 차량의 안전, 내구성, 신뢰성 관점에서 가혹한 조건의 진동내구 성능을 만족해야 한다. 특히, 동력계 핵심부품은 가진원인 노면 진동에 직접적으로 영향을 받으며 가혹한 작동환경에 빈번하게 노출되기 때문에 높은 진동내구 신뢰성이 요구된다. 진동으로 인한 부품의 내구성 문제는 고객 만족도와 직결되며, 이는 자동차 제조업체의 신뢰성과 브랜드 이미지에 큰 영향을 미친다. 따라서, 자동차 부품의 수명을 검증하기 위한 진동내구 신뢰성 평가의 중요성은 나날이 증가하고 있다. 또한, 자동차 부품 제조업체는 단축된 부품개발 요구사항을 만족하기 위해서 부품 개발기간 뿐만 아니라 내구성 검증을 위한 소요시간도 단축해야 한다.
현재의 진동내구 평가 기술은 주로 단축내구시험과 다축내구시험으로 나눌 수 있다. 단축내구시험은 비교적 단순하고 저렴한 비용으로 수행될 수 있으나, 실제 주행 조건에서 발생하는 복잡한 다축 진동을 재현하는 데 한계가 있다. 특히 차량의 파워트레인에 전달되는 진동부하는 다양한 방향으로 발생하며 진동의 크기도 예측할 수 없기 때문에 주로 한 방향의 진동만을 인가하는 방식인 단축진동시험은 적합하지 않다. 반면, 다축내구시험은 다양한 방향의 진동을 동시에 가하여 실제 주행 환경을 보다 빠르고 정확하게 모사할 수 있는 장점이 있다. 하지만 다축진동시험의 경우, 측정 데이터량이 많고 복잡한 주행모드를 재현해야 하기 때문에 가진 프로파일의 구현이 어렵고, 정밀한 분석이 필요하다(1~4). 따라서, 복잡한 주행모드별 진동내구 분석 시간을 단축하고 가진프로파일 생성 프로세스의 단계별 정립 및 데이터 신뢰성 향상을 위해서, 실차내구시험과 상관관계가 낮은 센서 및 이벤트로 데이터를 판별하여 제외하고, 상관관계가 높은 데이터 채택을 통한 데이터 정합성 향상이 필수적이다. 또한 기존 연구에서는 대부분 대상 시편의 총 가혹도 기준의 오차율을 최소화하기 위해 측정된 전체 이벤트로의 데이터를 적용하여 진동내구 가진 프로파일을 생성했다(5~7). 이러한 방식은 전체 이벤트로의 데이터를 기반으로 가혹도 오차를 산정하기 때문에, 일부 데이터는 오히려 오차율 증가의 원인이 될 수 있다. 따라서, 실차 데이터와의 패턴분석을 통해 유사성이 높은 이벤트로 데이터를 선정하여 총 가혹도를 산출함으로써, 기존 대비 목표 가혹도와의 오차율을 최소화할 수 있다.
일반적으로 내구(durability)시험과 피로(fatigue)시험은 대상시편의 공진점 또는 취약부를 시험모드로 선정하여 재료의 파손 및 균열의 시점에 대하여 S-N curve를 도출하거나 검증하는 방법으로 일반화되어 있다. 그렇지만 이 논문에서는 재질의 피로특성보다는 차량의 실도로부하조건(road-load condition)에서 주행 진동 특성을 통하여 차량의 주행내구성 보증(warranty)에 대한 신뢰성을 검증하는 방법을 제시하므로 위에서 언급한 일반적인 내구시험과 피로시험 방법과 유사하다고 판단하기는 어렵다. 또한, 이 논문에서 다루고 있는 프로파일 도출 방법은 기존 연구에서 방법론만을 제시하였지만(5~7), 이 논문에서는 이러한 방법에 대한 신뢰성에 대한 부분까지 고려하여 반영하였다. 즉, 기존 연구에서는 모든 특수로 데이터를 활용하여 실도로와의 오차율을 낮추는 방법을 제시하였지만, 이 논문에서는 8개의 이벤트로 데이터를 확보하여 실도로와의 유사성 분석을 통해 불필요한 이벤트로 데이터는 제외하고 상관관계가 높은 이벤트로는 선정하는 과정을 분석 및 적용하여 신뢰성 있는 방법론을 제시하였다. 또한, 가속도계 장착 후보 위치에서 다채널 진동 측정을 수행하고 진동 전달함수를 분석함으로써, 대상 구동계 부품에 대해 진동센서 마운팅 최적 위치를 선정하였다. 이러한 방법을 통하여 피로손상도와의 오차를 최소화하고, 가진 시간을 단축하기 위한 이벤트로 조합 방법을 적용함으로써 가진프로파일을 생성하고 가속내구시험 모드를 도출하는 방법을 제시했다. 제시된 방법이 적용된 가속도 센서 마운팅 최적 위치 선정을 통하여 최종 취약부 위치를 선정하게 되었고, 이벤트로 유사패턴 분석을 통하여 타겟 가혹도로 선정한 실도로와의 유사패턴을 갖는 이벤트로를 선정하여 기존 연구보다 이벤트로 선정 과정의 신뢰성 부분이 향상될 것이며 오차율 또한 줄어들 것으로 예상된다.
2. 진동내구 프로세스
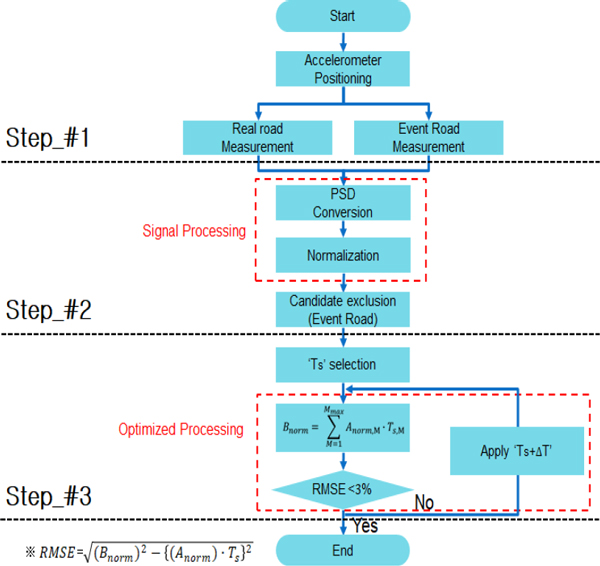
이 논문에서 제시하는 진동내구 가속화 방법은 실차 기반의 가속도 값을 통하여 실도로의 가혹도와 등가되는 이벤트로의 조합을 찾아내는 방법을 제시한다. 실도로와 이벤트로에서 계측된 가속도 데이터를 power spectral density(PSD)로 변환한 후 정규화 과정을 거쳐 이벤트로 조합을 찾아내는 방법을 제시하였다. 차량주행 진동과 같은 랜덤 진동신호의 주파수 도메인에서의 가혹도를 계산하는 경우, 랜덤 진동신호의 진폭의 변화량이 매우 크고 양수/음수의 천이가 반복적으로 발생하여 가혹도량으로 적용하기에 부적합하여, 파워 스펙트럴 밀도 함수(PSD)를 기반으로 가혹도를 계산하는 방법이 일반적으로 사용된다. 시험 대상품의 총 가혹도 값은 작동주파수 영역에서 각 주파수에 대해 합산되어 계산되며, PSD 곡선의 아래면적 크기 또는 진동의 평균제곱값에 비례한다(8,9). 이러한 부분을 적용하여 실도로와 등가되는 이벤트로 조합을 찾아가는 과정은 Fig. 1의 순서로 진행하였으며, 이 연구에서는 실도로와 이벤트로와의 최종 오차율이 3 % 미만이 되도록 함을 목표로 하였다.
2.1 가속도 센서 신호 처리 방법
실차 주행에서 계측된 데이터 신호를 활용하여 이벤트로 조합을 찾아가는 과정을 거치기 전에, 기본적으로 계측된 가속도 신호 처리 과정을 거치게 된다. 신호 처리 과정은 Siemens사의 Test.Lab을 통하여 수행하였다. 계측된 가속도 데이터를 FFT(fast Fourier transform)를 통해 주파수 변환한 후 가혹도 값인 PSD로 변환하였으며, 변환된 데이터를 정규화 과정을 거쳐 계측된 데이터를 행렬화 시켰다. 측정된 가속도 데이터를 이용하여 PSD 기반의 가혹도 크기를 산출하는 과정은 식 (1)로 표현이 된다. 그리고 계측된 가속도 데이터는 방향성을 갖는 벡터값이므로 식 (2)를 사용하여 정규화시켰다.
| (1) |
| (2) |
식 (1) 에서 a(f)는 측정된 가속도의 시간 데이터를 FFT를 통해 주파수 데이터로 변환한 각 주파수(f)별 가속도의 크기(amplitude)를 나타내며, 식 (2)에서 i는 각 시험모드에서의 모든 채널을 의미한다. 또한, Φ는 시험모드별로 정규화된 데이터의 전체 크기를 의미하므로 식 (3)과 같이 정의된다.
| (3) |
이 논문에서 B는 실도로에서의 계측된 PSD로 변환된 데이터를 의미한다. 그리고 N은 가속도 센서의 채널수를 의미한다. 따라서, 이 논문에서 3축 가속도 센서 총 3개를 사용하였으므로 실도로의 행렬은 9개의 채널수만큼 나타낼 수 있다. 그래서 각 채널에 대한 데이터를 식 (1), 식 (2)를 활용하여 식 (4)로 나타낼 수 있다. 또한, M은 계측된 이벤트로를 의미한다. 그렇다면 이벤트로 즉, A는 정규화 과정의 수식을 적용하여 식 (5)와 같이 표현이 가능하다.
| (4) |
| (5) |
실도로와 이벤트로의 실차 주행시험을 통한 계측된 가속도 값을 활용하여 B = A • T 라는 기본적인 수식을 도출할 수 있다. 여기서 T는 A인 이벤트로에서의 가혹도가 목표 가혹도인 B와 등가의 값을 가질 수 있는 운행 횟수를 의미한다. 이 논문에서의 찾고자 하는 최종 결과값은 T값이므로, 정규화된 A, B와 같이 정규화된 T값으로 변환하여 목표 결과값을 도출하게 된다. 여기에서 T의 정규화된 값은 Tnorm으로 규정하였다. 이 논문을 위해 계측된 실험 데이터는 N과 M의 개수가 같지 않으므로 Tnorm의 값을 찾는 방법은 식 (6)을 통하여 이벤트로의 조합을 찾아낸다. Tnorm을 찾아가는 방법은 우선적으로 Tnorm의 값은 정규화된 값이므로 0과 1사이의 값을 갖는다. 선정된 Tnorm값을 0에서부터 스텝 사이즈를 변경해가며 이벤트로의 조합을 선정한다. 식 (6)만을 적용하여 이벤트로의 조합을 찾았을 시 많은 조합의 결과가 도출되지만, 타겟으로 선정되어진 실도로의 값과의 오차율은 고려되지 않는다. 따라서, 최종적으로 식 (7)을 이용하여, 이 논문에서의 목표인 오차율 3 % 미만을 적용하게 된다면 후보 이벤트로를 기반으로 식 (6)과 식 (7)을 만족하면서 오차율이 목표치 이내에 수렴하는 이벤트로의 최종 조합을 찾아낼 수 있다.
| (6) |
| (7) |
식 (6)에 대해 도출된 Tnorm값은 정규화된 값이므로 최종적으로 T로의 변환이 필요하다. 앞서 기술한 수식들과 A, B를 활용한 Anorm, Bnorm의 식 (8), 식 (9)와 B = A • T 수식을 활용하여 최종 T값을 도출하였다.
| (8) |
| (9) |
T값의 최종 수식은 식 (10)과 같이 유도된다.
| (10) |
식 (10)에서 ΦA, ΦB는 각각 이벤트로와 실도로에서 계측된 가속도 데이터를 식 (3)에 적용하여 도출된 값을 의미한다(5,6).
2.2 가속도 센서 위치 선정
이 논문에서는 주요 계측 신호인 가속도 신호를 기본 데이터로 활용하고 있다. 그러므로 가속도 계측 위치는 매우 중요하다. 위치 선정 방법은 취약부라 예측되는 모든 위치에 대하여 가진과 응답을 실험적으로 진행하는 것이다. 그렇지만 이러한 방법은 많은 시간이 소요된다. 따라서 차량 주행 시 진동의 주요 원인인 노면진동의 전달경로를 고려하여 가진 위치를 선정하였고, 취약부라 예측되는 지점에서의 응답 위치를 선정하여 실험을 진행하였다. 이러한 방법으로 시험을 수행하기 위해서는 주파수응답 특성에서 선형적(linear)이고 양방향성 관계(bilateral)가 성립되어야 하는데 식 (11) 맥스웰의 상호성이론(Maxwell’s reciprocity theorem)에서의 가진위치(i)와 응답위치(k)와의 관계성을 활용하게 된다면 신뢰성 있는 위치 선정을 할 수 있게 된다(10). 즉, 모든 위치에서 가진과 응답에 대한 실험을 진행한 것과 동일한 결과값을 도출해 낼 수 있다.
| (11) |
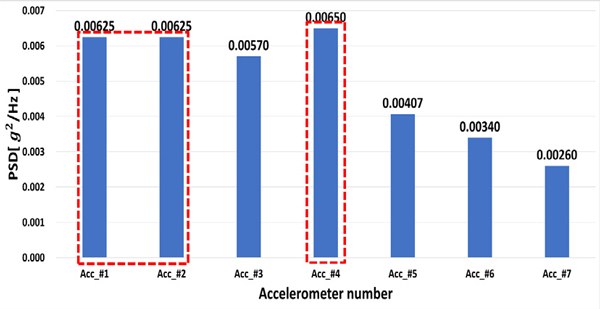
식 (11)에서, H는 가진위치(i)와 응답위치(k)사이의 전달함수를 의미한다. 이러한 실험 방법을 적용하기 위하여 Fig. 2와 같이 실험 환경을 구성하였다. 일반적으로 센서 위치 선정 방법의 경우 대상 시편에서의 특성만을 파악하기 위하여 구속조건이 없는 상태(free-free condition)로 진행하여야 한다. 그렇지만, 이 실험에서는 가진 시 모든 가속도 센서에서의 응답성을 상대비교로 진행하므로 Fig. 2에서와 같이 수직축의 최소한의 구속조건만 작용한 상태로 시편을 지지하였다. 대상 시편은 국내 완성차 업체의 그랜져 IG 차량의 파워트레인을 선정하였고, 계측과 가진은 각각 Siemens사의 Test.Lab과 PCB사의 임팩트해머(model:086C03)로 환경을 구성하였다. 가속도 센서 장착 위치는 취약부로 예측되는 위치를 후보군으로 선정하여 Fig. 3과 같이 7개의 위치를 후보군으로 선정하였다. 또한, 노면 진동의 전달경로를 고려하여 가진 포인트는 Fig. 3(a) top view에서의 3번 위치로 선정하였다. 계측된 데이터는 위치별 상대 비교로 분석하였으며, Fig. 2에서의 Z축 방향 즉, 차량 기준에서의 수직 방향으로 분석하였다. 수직 방향의 데이터를 기준으로 분석한 이유는 차량이 주행 시 타방향에 비해 수직 방향에서의 진동이 차량 내구성에 주요한 영향을 주므로 수직 방향의 데이터를 비교군으로 선정하였다. Fig. 4는 각 위치에서 측정된 가속도 데이터를 식 (1)에 적용하여 계산된 가혹도 데이터의 크기를 비교한 것이다. 인가하는 가진력의 크기 및 위치는 동일하기 때문에 특정 위치에서의 가혹도가 높다는 것은 동일한 가진력 대비 진동응답의 크기가 다른 위치에 비해 큰 것을 의미하며, 내구시험 진행 시 파손될 가능성이 상대적으로 높은 취약부로 분석된다. Fig. 4의 결과에서 1번, 2번, 4번에서의 가혹도 크기가 가장 높게 측정되었으므로 최종적으로 가속도 센서의 최적 위치로 선정하였다.
2.3 주행 모드 선정 및 데이터 계측
실차 주행시험에서 가속도 센서는 2.2절에서 선정한 1번, 2번, 4번 위치로 Fig. 5와 같이 장착하였으며, 대상 차량 또한 동일한 부품이 적용된 국내 완성차 업체의 그랜져 IG 차량으로 선정하였다.
주행 모드는 실도로와 이벤트로 두 가지로 구분하였으며, 실도로는 국내도로와 운전자의 상황을 고려하여 고속도로, 비포장로, 시내도로, 포장로(국도+지방도)를 Table 1의 비율로 Table 2와 같이 총 1400 km를 주행하였다.
이벤트로 시험은 한국자동차연구원에서 보유 중인 주행로 PG(proving ground)에서 진행하였으며, Fig. 6과 같이 총 8개의 이벤트로에 대하여 30 km/h 정속으로 시험 모드를 선정하였다. 또한, 진동내구의 가속화를 위한 이벤트로의 1 cycle의 소요시간 및 거리 또한 주요하게 사용되므로 Table 3과 같이 정리하였다.
일반적으로 실도로의 주파수 성분은 150 Hz 미만에서 모든 주요 주파수 성분을 갖는다. 그리하여 실차 데이터 계측은 이러한 부분까지 고려하여 512 Hz의 bandwidth로 설정 후 데이터 계측을 진행하였다. 이벤트로의 데이터 신뢰성 확보를 위하여 총 3번 이상의 주행을 진행하였고 데이터의 경향성 및 유사성을 고려하여 대표 이벤트로의 데이터를 선정하였다.
2.4 실도로와의 상관관계 분석을 통한 이벤트로 후보군 제외
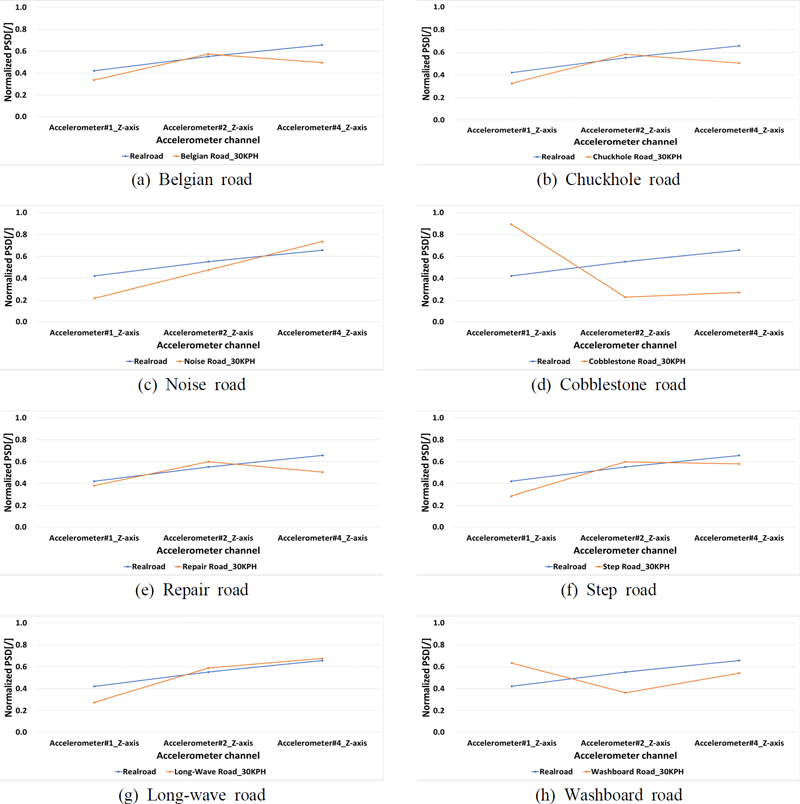
모든 이벤트로의 특성이 실제 타겟인 실도로 데이터와의 유사성이 있다고 확신할 수 없다. 따라서, 데이터 유사성 및 신뢰성 향상과 타겟 가혹도와의 오차를 줄이기 위해서, 실도로 데이터와 상관관계가 낮은 이벤트로 데이터를 판별하여 제외하는 과정을 수행하였다. Table 4와 Table 5는 데이터 상관관계 비교분석을 위해서, 실도로와 각 이벤트로의 가속도 측정 데이터를 식 (1) ~ 식 (5)를 활용하여 정규화한 데이터로 정리하였다. Table 4의 경우 실도로의 주행 루트로 선정한 고속도로부터 포장로까지의 모든 주행 조건에 대한 총 가혹도로 규정하였으므로 하나의 정규화된 데이터로 정리하였다. Fig. 7은 주 가진 방향인 수직 방향을 기준으로 실도로 데이터와 이벤트로를 비교한 그래프이다. Fig. 7(d)와 Fig. 7(h) 결과와 같이 자갈길로와 빨래판로는 실도로 데이터와 음의 상관관계를 보이므로 후보군에서 제외하였다. 그리고 실도로 데이터의 2번과 4번은 상승 경향성을 보이고 있으나, 반대의 경향성을 보이는 Fig. 7(a) 벨지안로, Fig. 7(b)표준악로, Fig. 7(e) 보수로, Fig. 7(f) 단차로까지 후보군에서 제외하였다. 최종적으로 음의 상관관계를 보이는 후보군과 실도로와 유사 경향성이 아닌 후보군을 제외하고 Fig. 7(c) 소음로와 Fig. 7(g) 장파형로를 최종 후보군으로 선정하였다.
2.5 선정된 이벤트로의 Cycle 값 도출
앞서 제시한 2.1절의 정규화된 이벤트로 조합 및 가진시간을 구하기 위해 타겟 가혹도와 이벤트로 데이터를 통해 도출된 가혹도의 RMSE가 최소화되도록 최적화된 모델의 파라미터를 구하는 방법인 최소자승법(least square method)을 적용하였다. 최소자승법은 어떤 계의 해를 근사적으로 구하는 방법으로, 근사적으로 구하려는 해와 실제 해의 오차의 제곱의 합이 최소가 되는 해를 구하는 방법이다. 이 방법은 이 논문에서와 같이 목표 데이터는 결정되어 있으나 다입력 시스템에 대해 정확한 해를 구할 수 없는 경우에 유용하게 사용될 수 있으며, 비선형 시스템의 해를 추정하는 데에도 사용된다(11).
이 기법은 식 (6)에서 Tnorm의 값을 구하기 위하여 식 (7)의 에러 도출 수식에 적용이 가능하다. 그러나 최종 Tnorm값은 최적해를 구하는 과정에서 음수가 될 가능성이 있다. T값의 경우 이벤트로의 cycle 즉, 운행 시간에 대한 값이며 음의 수가 나올 수 없으므로 최종적으로 구하고자 하는 T값의 해가 0 또는 양수만을 가질 수 있도록 T값을 초기값 0부터 미소량만큼 증가시키면서 최종 목표인 이벤트로 조합과 운행 시간에 대한 값을 Table 6과 같이 도출하였다.
Table 6과 같이 이벤트로의 1 cycle에 대한 운행 시간과 횟수(T)를 조합하면 1400 km에 대한 시간은 약 5.8시간 소요된다. 만약, 1400 km를 실제 주행할 시 고속도로의 정규속도인 100 km/h의 속도로 운행한다고 가정하면 14시간이 소요된다. 2.3절에서 선정한 실도로 조건은 고속도로의 정규속도보다 낮은 정규속도의 주행 모드가 포함되어 있다. 그래서 실주행 시 14시간 이상의 시간이 소요되므로 이벤트로의 조합은 내구시험의 가속화가 가능하다.
Table 6에서의 조합된 이벤트로와 T값을 통하여 이벤트로의 총 가혹도값(A • T)을 구할 수 있다. 계측된 가속도 데이터를 식 (1)에 적용하여 선정된 각 이벤트로의 채널별 가혹도를 Table 7과 같이 각 채널별 9개의 값으로 정리하였다. 각 이벤트로 1 cycle 당 가혹도는 9개의 채널의 가혹도를 합하여 구할 수 있다. 그리하여 각 이벤트로의 1 cycle에 대한 가혹도값은 Table 8과 같이 도출되었다. 같은 방법으로 실도로의 채널별 가혹도값을 Table 9와 같이 정리하였다. Table 6에서 선정된 T값과 Table 8의 1 cycle에 대한 가혹도값을 식 (6)에 적용하여 이벤트로드 총 가혹도값을 구하였으며, Table 9에서의 모든 채널의 합을 통하여 실도로의 총 가혹도를 구하였다. 따라서 실도로 총 가혹도(B)와 이벤트로드 총 가혹도(A • T)는 Table 10과 같이 각각의 최종 가혹도를 구하였다.
최종 분석 결과, 선정된 이벤트로 총 가혹도는 실도로 가혹도 대비 오차율이 2.8 %로 나타났으며, 목표치인 3 % 미만을 만족하게 되었다.
3. 결 론
이 논문에서는 자동차의 파워트레인 핵심부품의 진동 내구성을 실험실 환경에서 평가하기 위한 가속내구 시험 모드 개발 방법을 제시하였다. 기존의 방법과 비교할 때 목표 피로손상도와의 오차를 최소화하고 가진 시간을 단축하면서 신뢰성 있는 연구결과를 도출하기 위하여 가속도 센서 최적 위치 선정 프로세스와 이벤트로 선정 방법을 제시하였다. 가속도 센서 최적 위치 선정기법을 통해 동일 가진력 대비 진동응답의 크기가 상대적으로 높은 위치를 대상 시편의 취약부로 도출하였으며, 이벤트로 조합을 통해 실도로와 이벤트로와의 데이터 정합성을 향상시키고 오차율을 개선하였으며, 이벤트로 데이터의 신뢰성 향상과 분석 시간 단축 방법을 제시하였다.
제시된 방법을 통해 진동내구 가진시간을 단축하고 차량 부품의 내구 신뢰성을 향상시킬 수 있을 것으로 기대된다. 또한, 현재 트랜드인 전력기반 차량의 모터, 감속기와 같은 파워트레인부에도 적용이 가능할 것으로 판단되며, 향후 채널별 가혹도 상관관계 분석, 실도로와 이벤트로의 주파수 분석을 통하여 진동내구 가속화의 신뢰도를 높여갈 수 있을 것으로 기대된다.
References
- ISO, 2018, Road Vehicles — Environmental Conditions and Testing for Electrical and Electronic Equipment for Drive System of Electric Propulsion Vehicles — Part 3: Mechanical Loads, International Organization for Standardization, ISO 19453-3:2018, Geneva, Switzerland.
- KATS, 2006, Vibration Testing Methods for Automobile Parts, Korean Agency for Technology and Standards, KS R 1034:2006, Chungcheongbuk-do, Korea.
-
Yoon, J. S., 2018, Study of Vibration Fatigue Test for Urea Tank of Diesel Vehicle Considering Vibration Characteristics, Journal of Applied Reliability, Vol. 18, No. 3, pp. 213~219.
[https://doi.org/10.33162/JAR.2018.09.18.3.213]

- Kim, C. J., 2016, Time Domain Severity Calculation Method for Selecting Short-axis Vibration Test Specifications, Journal of KSNVE, Vol. 26, No. 4, pp. 21~24.
-
Kim, C.-J., Kang, Y. J. and Lee, B.-H., 2012, Generation of Driving Profile on a Multi-axial Vibration Table for Vibration Fatigue Testing, Mechanical Systems and Signal Processing, Vol. 26, pp. 244~253.
[https://doi.org/10.1016/j.ymssp.2011.07.018]

-
Bae, C.-Y., Kim, C.-J., Lee, D.-W., Lee, B.-H. and Na, B.-C., 2008, Signal Processing for Multiaxial Vibration Fatigue Test on Vehicle Component, Transactions of the Korean Society for Noise and Vibration Engineering, Vol. 18, No. 3, pp. 368~374.
[https://doi.org/10.5050/KSNVN.2008.18.3.368]

-
Kim, C.-J., Lee, B.-H. and Kim, G.-H., 2005, Generating Method of the Input Profile in the MAST System, Transactions of the Korean Society for Noise and Vibration Engineering, Vol. 15, No. 9, pp. 1070~1076.
[https://doi.org/10.5050/KSNVN.2005.15.9.1070]

- Kumar, S. M., 2008, Analyzing Random Vibration Fatigue, ANSYS Advantage, Vol. 2, No. 3, pp. 39~42.
-
Dirlik, T. and Benasciutti, D., 2021, Dirlik and Tovo-Benasciutti Spectral Methods in Vibration Fatigue: A Review with a Historical Perspective, Metals, Vol. 11, No. 9, 1333.
[https://doi.org/10.3390/met11091333]

-
Findeisen, D., 2000, System Dynamics and Mechanical Vibrations: An Introduction, Springer, Berlin, Germany.
[https://doi.org/10.1007/978-3-662-04205-2]

- Chapra, S. C. and Canale, R. P., 2020, Numerical Methods for Engineers, 8th Edition, McGrawhill, NY, United States.

Hyosung Kim is a M.S. student in the Department of Mechanical Engineering at Kyungpook National University(KNU). He is also a current researcher at Korea Automotive Technology Institute. His research interests are Noise and Vibration.

Gwangmin Park is principal researcher at Korea Automotive Technology Institute. He received Ph.D. degree in Energy engineering from KNU. His research interests are control, AI, NVH and power electronics.

Yongrae Roh is professor in the School of Mechanical Engineering, KNU. His research area includes the development of acoustic and vibration transducers for mechanical and multi-physics systems.