수중 평판의 등가 음향임피던스 역산을 위한 간이수조 시험

1. 서 론

표적 강도(target strength, TS)는 수중함의 스텔스 성능(stealth performance)에 영향을 미치는 핵심 설계 인자이며, 수중함의 TS가 높을수록 위협 세력으로부터의 피탐 확률이 증대된다. 이에 선체 외판에 흡음 재료, 음향 타일 등의 음향 재료를 부착하여 수중함의 TS 수준 저감을 도모하고 있으며, 이와 같은 음향 재료의 반사, 투과 및 흡음 특성을 파악하기 위한 일련의 연구가 수행된 바 있다.

Audoly and Giangreco는 수조 내 음향 평판에 음파를 수직 입사하여 음향 재료의 반사, 투과 및 흡음 특성을 평가하는 시험 방법을 제시하였다⁽¹⁾. 또한, Piquette and Forsythe는 임피던스 튜브를 활용하여 임의 음향 재료의 반향음 감소 및 삽입 손실 특성 산정 결과를 제시하였다⁽²⁾. Shin et al.은 표적 반향음 및 투과음 저감을 위한 음향 재료의 반향음 감소, 투과 손실 등의 음향성능을 정량적으로 평가하기 위한 시스템을 구축하고, 그 유효성을 검증하였다⁽³⁾. 아울러, Jung et al.은 함정에 탑재되는 소나 돔 제작 재료의 투과 손실 특성 파악을 위한 실험을 설계하고, 측정 대상 시편의 회전에 따른 음의 회절 영향, 시편 크기, 투과 손실 수준 산정 방법 등을 검토하였다⁽⁴⁾.

수중함의 설계 및 건조 단계에서 TS 수준을 정도 높게 예측하기 위해서는 선체 및 이에 부착되는 음향 재료의 등가 음향임피던스에 대한 엄밀한 반영이 필요하다. 이를 위해서는 임의 음향 재료 내 음속에 관한 정도 높은 평가 기법이 요구되며, 이와 관련해서는 Gartland et al.이 대형 수조에서 계측한 음향 재료의 반향음 특성을 이용하여 유체 모델에 기반한 임의 음향 재료의 등가 복소 음속 역산 기법을 정립한 바 있다⁽⁵⁾.

한편, 잔향수조, 예인수조 등과 같은 대형 수조에서는 상기와 같은 실험의 설계 및 구성이 다소 어려우므로, 함의 표적 강도 수준 저감을 위해 선체 표면에 부착되는 음향 재료의 등가 임피던스 평가를 위한 대형 수조에서의 실험 이전에 시험 환경 구축이 비교적 용이한 간이수조 및 무지향성 수중 음향 센서를 이용한 상기 방법론의 재현 및 검증 연구가 필요하다.

이에, 이 논문에서는 간이수조 환경에서 임의 음향 재료의 반사율을 계측하고, 이의 결과를 활용하여 등가 음향임피던스를 역산하기 위한 기초 실험 연구를 수행하였다. 이를 위해 무지향성 음원을 이용한 반사율 계측용 간이수조 시험 환경을 구축하고, 이를 활용한 음향 재료의 등가 복소 음속 및 음향임피던스 산정 방법과 이의 절차를 정립하였다.

2. 이론적 배경

2.1 임의 재질 평판의 반사율

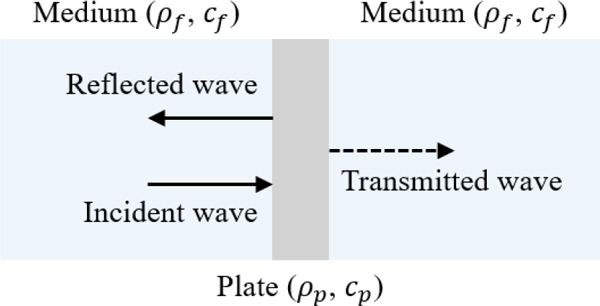
평판에 수직 입사된 평면파는 Fig. 1에 나타낸 바와 같이 반사파 및 투과파로 나뉘어 매질로 전파된다. 이때, 매질 내에서의 손실을 무시하면 평면 수직 입사파에 대한 반사율은 식 (1)로부터 산정할 수 있다^(5,6).

Fig. 1

Incident, reflected and transmitted waves

$\[ R\left(\omega \right)=\frac{p_r\left(\omega \right)}{p_i\left(\omega \right)}=\left[\frac{Z_p^2-Z_f^2}{j2Z_p{Z}_f\cot \left(k_p{t}_p\right)+Z_p^2+Z_f^2}\right]\varphi \]$

(1)

여기서, 위상차 ϕ는 식 (2)에 나타낸 바와 같이 정의한다.

$\[ \varphi =e^{-j\left(2\frac{\omega }{c_f}{r}_p-\omega \delta \right)} \]$

(2)

이때, 수조에서의 실험으로부터 획득한 반사율 계측 결과를 식 (1)에 대입하고, 이를 수치 해석하면 평판 내 복소 음속을 역산할 수 있다.

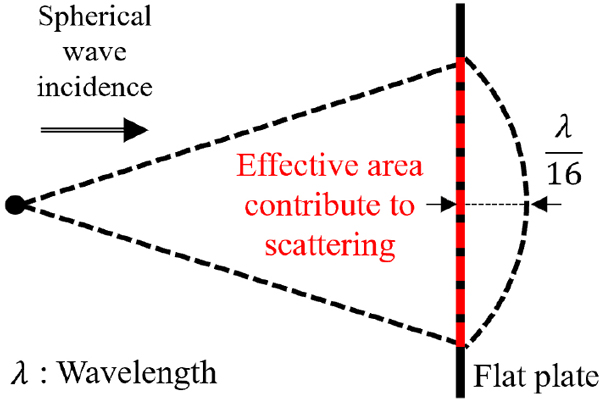
이 연구에서는 평면파의 수직 입사를 가정하는 식 (1)에 대해 무지향성 음원을 활용한 구면 입사파의 적용 가능성을 검토하였다. 구면파가 입사되는 평판은 근거리장 효과에 따른 위상차를 반영하기 위해 구면파의 형태로 변형된 곡판에 평면파가 입사하는 조건으로 근사할 수 있다. 이와 같은 경우엔 평판에 평면파가 입사하는 경우와는 다르게 Fig. 2에 나타낸 바와 같이 평판 산란 수준에 지배적으로 기여하는 유효 산란 영역을 정의할 수 있으며⁽⁷⁾, 상기 유효 산란 영역이 평판 내에 위치하면 구면 입사파를 평면 입사파로 근사할 수 있다.

Fig. 2

Effective scattering area of a flat plate under spherical wave incidence condition

후술할 실험에서의 계측 대상 주파수 중 파장이 가장 긴 45 kHz의 경우, 유효 산란 영역에 해당하는 한 변의 길이는 약 0.0578 m로써 평판의 한 변 길이인 0.2 m 대비 약 3.46배 작음을 알 수 있다. 아울러, 주사음의 주파수가 높아질수록 유효 산란 영역이 좁아지는 경향이 있음을 고려하여, 이 연구에서는 무지향성 음원으로부터 방사된 구면파는 평면 입사파로 근사할 수 있다고 가정하였다. 한편, 이와는 별개로 평판 모서리에 의한 회절음과 평판 내부 다중 반사에 의한 평판 반사음은 평판 반사율 산정에 반영되어야 하나, 이 연구에서는 이들의 음압 기여도가 평판 표면에 의한 1차 반사음 대비 무시할 수 있을 정도로 작다고 가정하였다.

아울러, 무지향성 음원으로부터 방사된 음의 구면 확산에 따른 전달 손실은 식 (3)에 나타낸 바와 같이 계측한 복소 반사 음압을 보정하여 고려하였다.

$\[ p_r^{\text{'}}\left(\omega \right)=\frac{r_s+2r_p}{r_s}{p}_r\left(\omega \right) \]$

(3)

여기서, 소음원-수음점 및 수음점-평판 간 거리인 r_s 및 r_p는 후술할 실험 설계에 따라 각각 0.1 m 및 0.15 m로 설정하였다.

3. 등가 음향임피던스 역산 절차

임의 재질 평판의 등가 음향임피던스는 간이수조 내 평판 반사율 계측 결과를 이용한 다음의 절차로부터 실험적으로 평가할 수 있다.

(1) 간이수조 내 무지향성 수중 음향 송신기/청음기 및 임의 재질 평판 위치

(2) 수중 음향 송신기로부터 다섯 파장 길이의 정현파 신호 방사

(3) 수중 청음기를 활용하여 시간이력 입사파 및 반사파를 동일 위치에서 계측

(4) 시간이력 신호에 대한 교차상관으로부터 입사파 및 반사파 식별 후⁽⁹⁾, 정현파의 형태가 잘 나타나는 2개 파장만을 추출

(5) 추출한 입사파 및 반사파 2개 파장 신호 각각에 대해 입사 및 반사파 상호 간 계측 시간 지연이 없도록 (δ = 0) zero-padding하여 주파수 해상도를 확보한 후, 고속 Fourier 변환하여 주파수역 신호로 변환

(6) 입사파 및 반사파의 주파수 영역 복소 음압을 활용하여 평판 반사율 평가

(7) 평가된 반사율을 반영한 식 (1)에 대한 수치해석으로부터 평판 내 복소 음속 역산

(8) 평판 내 복소 음속을 활용하여 식 (9)에 나타낸 바와 같이 임의 재질 평판의 등가 음향임피던스 산정

4. 간이수조 시험 환경 구축

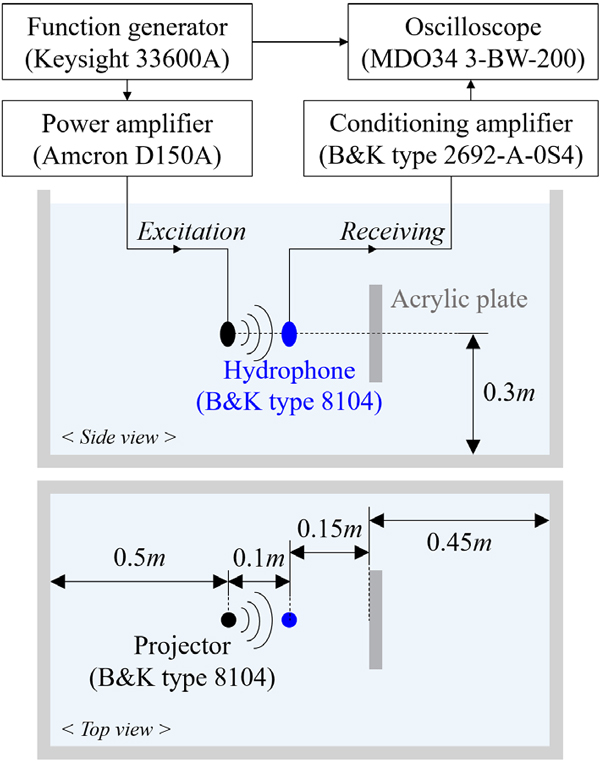
이 연구에서는 시험 환경 구축이 비교적 용이한 간이수조 및 무지향성 음원을 활용하여 평면파의 수직 입사를 가정하는 식 (1)을 통한 임의 재질 수중 평판 등가 음향임피던스 역산 방법의 적용성을 실험적으로 검토하였다. 이를 위해 길이, 폭, 높이가 각각 1.2 m, 0.6 m, 0.62 m인 간이수조를 활용하여 한 변의 길이 및 두께가 각각 0.2 m 및 0.01 m인 정사각 아크릴 평판의 반사율을 측정하였다. 입사파 및 반사파 음압은 무지향성 수중 청음기 B&K type 8104를 활용하여 측정하되, 이들을 단일 시험 내 동시 계측하여 반복 계측에 의한 불확실성을 배제하였다. 한편, 음원 및 수음 센서의 음향 중심 간 거리는 근거리장 효과로 인해 음파의 한 파장 대비 매우 커야하나 음향 공간이 협소한 간이수조 환경을 고려하여 가장 낮은 계측 주파수 45 kHz의 파장 0.033 m의 약 3배에 해당하는 0.1 m로 설정하였다. 이로부터 선정된 평판 및 음향 센서의 위치를 반영한 실험 구성은 Fig. 3 및 Fig. 4에 나타낸 바와 같다.

Fig. 3

Experiment configuration

Fig. 4

Acoustic sensors and plate arrangement in the simple water tank

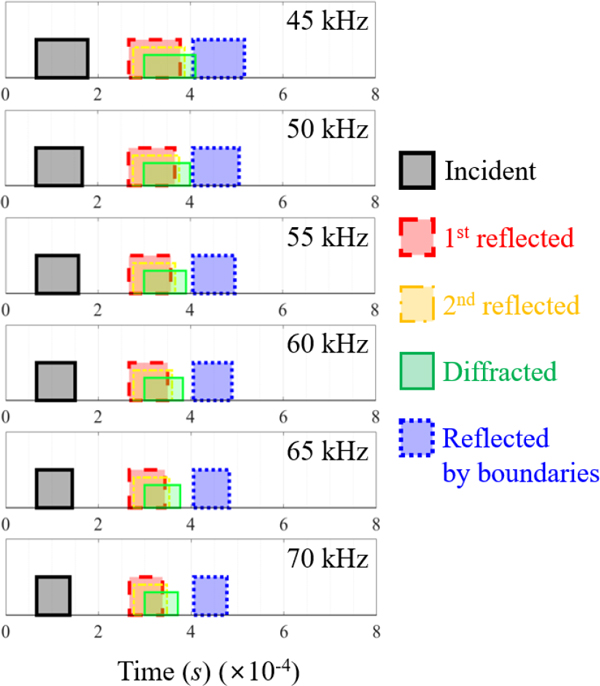
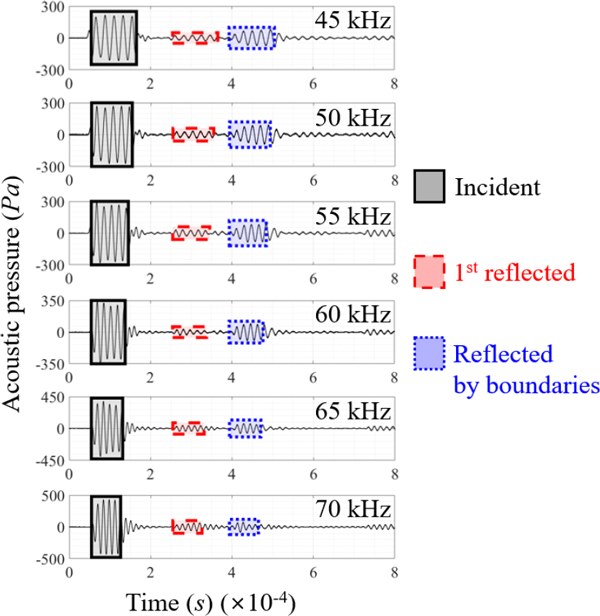
한편, 평판 한 변의 길이는 가장 낮은 계측 주파수 45 kHz 파장 대비 약 6배이며, 이로부터 평판에 의한 산란은 고주파수 영역에서의 산란 현상으로 간주할 수 있다. 즉, 평판 산란파는 표면에 의한 1차 반사음, 내부 반사음, 모서리에 의한 회절음 등으로 구분하여 고려할 수 있으며, 계측 대상 주파수별 입사음(incident), 평판 표면에 의한 1차 반사음(1st reflected) 및 내부 다중 반사에 의한 평판 반사음(2nd reflected), 간이수조 벽면, 바닥면, 자유수면 등 음장 경계 반사음(reflected by boundaries) 및 모서리에 의한 회절음(diffracted) 각각에 대한 도달 시간을 모의한 결과는 Fig. 5에 나타내었다.

Fig. 5

Signal arrival time simulation for the incident, reflected, diffracted waves

이때, 각 음파 성분이 수음 지점에 최초 도달하는 시간은 Fig. 3에 나타낸 시험 환경에 따른 음파 성분별 전파 경로의 길이 및 음속을 이용하여 산정하였고, 음파의 폭은 각 주사 주파수별 5개 파장의 길이로부터 결정하였다.

이로부터 입사음, 평판 표면에 의한 1차 반사음 및 음장 경계에 의한 반사음은 상호 식별이 가능한 반면, 평판 내부 반사음 및 회절음은 부분적으로 평판 표면 반사음과 중첩되어 상호 간 식별이 곤란함을 확인할 수 있다. 그러나 다중 투과 및 반사를 통해 수음 지점을 지나는 평판 내부 반사음과 모서리에 의한 회절음의 크기는 평판 표면에 의한 1차 반사음 대비 무시할 수 있을 정도로 작다고 가정하였고, 실험 설계에 있어서 이들의 기여도는 별도 고려하지 않았다.

상기 계측에 있어서 아크릴 평판 반사율 측정 대상 주파수는 45 kHz ~ 70 kHz 범위를 5 kHz 간격으로 나눈 6가지로 선정하고, 수중 음속이 1500.43 m/s일 때 이들 계측 주파수 각각에 대한 정현파 파장을 산정하여 Table 1에 함께 나타내었다.

Table 1

Measurement cases on equivalent acoustic impedance inversion of acrylic square plate

이때, 무지향성 수중 음향 송신기로부터 방사되는 주사 신호는 계측 대상 주파수 각각에 대해 다섯 파장 길이의 정현파 신호로 생성하여 아크릴 평판 반사율 측정에 활용하였다. 아울러, 이산 데이터의 샘플링 속도는 시간 분해능에 의한 계측 오차를 고려하여 2.5 GSample/s로 설정하였고, 이에 따른 계측 시간 간격은 0.4 ns이다.

5. 시험 결과 및 고찰

수중 청음기로부터 획득한 시간이력 수음 신호는 Fig. 6에 나타내었다.

Fig. 6

Received incident and reflected signals

시간이력 음압 계측 결과로부터 평판 표면에 의한 1차 반사음의 형태는 입사파의 형태와 유사함을 확인할 수 있다. 이에, 평판 내부 반사음과 모서리에 의한 회절음의 크기는 평판 1차 반사음 대비 무시할 수 있을 정도로 작다고 판단하였고, 이 연구에서는 평판 반사율 산정에 있어 이들의 음압 기여도를 별도 반영하지 않았다. 아울러, 입사파 및 평판 표면에 의한 1차 반사파에 대한 음 도달 시간 분석 결과는 계측 결과와 부합성이 높으며, 이로부터 수중 음향 센서 및 평판 배치에 관한 실험 설계가 양호함을 확인할 수 있다. 한편, 음장 경계에 의한 반사파 도달 시간은 음 도달 시간 분석 결과 대비 다소 차이가 있음을 확인할 수 있는데, 이는 간이수조의 벽면 및 바닥면과 자유수면에서 각기 반사된 음파의 전달 경로 및 길이가 서로 다르기 때문인 것으로 판단한다.

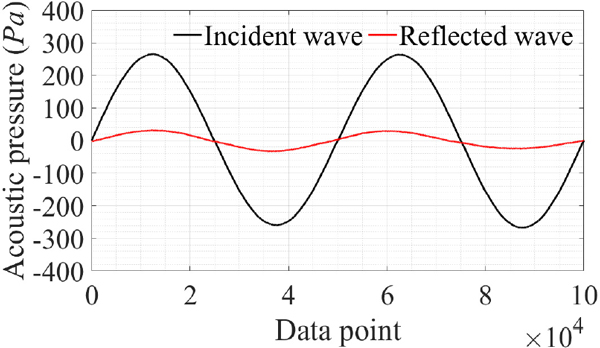
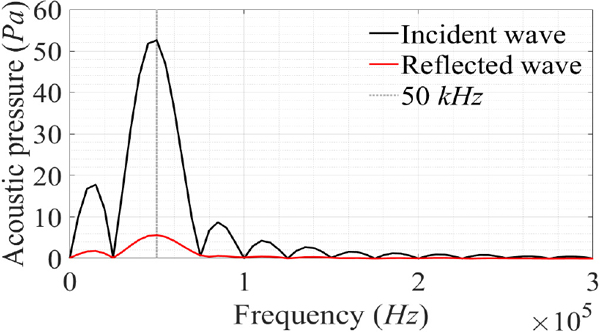
상기 시간이력 수음 신호로부터 입사파 및 아크릴 평판에 의한 반사파 성분을 상호 간 교차상관을 통해 식별한 후, 수신한 다섯 파장 중 음압의 피크치가 안정적으로 나타나는 세 번째 및 네 번째 파장만을 추출한 결과는 Fig. 7에 예시하였다. 아울러, 입사파 및 반사파 시간이력에 대해 주파수 해상도 확보를 위한 zero-padding 후, 이들 각각에 대해 고속 Fourier 변환한 결과는 Fig. 8에 예시하였다.

Fig. 7

Example of incident and reflected pressures in time-domain: Case 2, 50 kHz

Fig. 8

FFT results for incident and reflected waves: Case 2, 50 kHz

또한, 6가지 계측 경우 각각에 대해 주사 신호 주파수에 해당하는 입사파 및 반사파 복소 음압 평가 결과는 Table 2에 나타내었다.

Table 2

Complex acoustic pressures of incident and reflected waves for six measurement cases

아울러, 복소 음압 계측 결과를 활용하여 아크릴 평판의 복소 반사율을 평가한 결과는 Table 3에 나타내었다. 한편, 상기 복소 반사율을 식 (1)에 대입하여 평판 내 복소 음속을 수치적으로 역산한 결과는 Table 4에 나타내었고, 이와 함께 평판 내 음속에 해당하는 복소 음속의 실수부와 식 (10)을 이용한 음속 산정 결과인 2109.66 m/s의 상호 차이를 산정하여 표에 정리하였다.

Table 3

Complex reflectivity of the acrylic flat plate

Table 4

Inversion results on complex compressional wave speeds in the acrylic flat plate

이때, 식 (1)에 대한 수치해석에 있어서 물의 밀도는 1000 kg/m³로 설정하였고, 해석 초기값은 식 (10)으로부터 산정한 아크릴 평판 내 음속과 유사하게 2100 m/s로 부여하였다.

여기서, Re(c_p)는 복소 음속의 실수부로써 아크릴 평판 내 음속을 나타내며, 이의 산정을 위한 아크릴의 탄성 계수, 밀도 및 Poisson 비는 각각 3.3 GPa, 1190 kg/m³ 및 0.35로 적용하였다⁽¹⁰⁾.

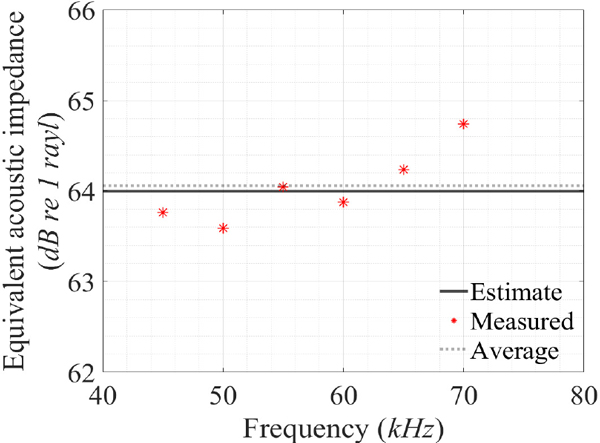
한편, 상기 결과 및 식 (9)로부터 아크릴 평판의 등가 음향임피던스를 평가한 결과는 Table 5에 나타내었고, 이들 결과(measured, average)와 식 (10)으로부터 산정한 아크릴 평판의 등가 음향임피던스(estimate)를 비교하여 Fig. 9에 도시하였다.

Table 5

Evaluation results on the equivalent acoustic impedance of acrylic flat plate

Fig. 9

Equivalent acoustic impedance of acrylic plate

이로부터 반사율 계측 기반 아크릴 평판의 등가 음향임피던스 평가 결과는 재료 물성 기반 산정 결과 대비 최대 차이가 19.7 %이며 주파수에 따라 상호 간 차이가 다름을 확인할 수 있는데, 이는 6가지 주사 주파수 각각의 매질 내 파장이 서로 달라 평판 표면에 의한 반사음의 위상 간섭 효과가 상이하게 반영되었기 때문인 것으로 사료한다. 아울러, 이와 같은 차이는 식 (1)이 수중 평판에 대한 평면파의 수직 입사를 가정하는 데에 반해, 이 연구에서는 구면파를 방사하는 무지향성 소음원을 활용하여 평판 모서리에 의한 산란, 전단파에 의한 근거리장 효과, 평판 내부 2차 반사의 영향 등을 엄밀하게 반영하지 못했기 때문인 것으로 사료한다. 한편, 흡음, 반사 및 투과 등 재료의 음향 특성 연구에서 널리 활용되는 대수적 표현에 있어서 상호 결과 간 최대 차이는 약 0.7 dB이며, 이로부터 아크릴 평판의 등가 음향임피던스 평가 결과의 상호 간 부합성이 높다고 판단한다.

아울러, 이 연구에서는 음장 규모가 작은 간이수조를 이용한 실험을 수행하여 입사파 및 평판 반사파, 음장 경계에 의한 반사파 등을 상호 식별하기 위해 고주파수 대역의 주사음을 활용하여 아크릴 평판의 등가 음향임피던스를 평가하였으나, 상대적으로 음장 규모가 큰 잔향수조, 예인 수조 등에서 동일한 방법으로 실험을 수행하면 비교적 저주파수 영역에서의 평판 등가 음향임피던스 평가도 가능할 것으로 사료한다. 한편, 평판 두께 및 주사음 주파수 파장 간 관계에 따라 음의 반사 대비 투과 현상이 지배적으로 나타나는 경우, 평판 반사음 계측이 곤란하여 이 연구에서 적용한 방법을 통한 임의 재질 평판의 등가 음향임피던스 평가는 다소 어려울 것으로 사료한다.

6. 결 론

이 논문에서는 함의 표적 강도 수준 저감을 위해 선체 표면에 부착되는 음향 재료의 등가 임피던스를 수중 평판 반사율 계측 결과로부터 역산하는 방법의 유효성에 관한 기초 실험 연구를 수행하였다. 이를 위해 간이수조 내 아크릴 평판의 반사율 계측을 통한 등가 음향임피던스 역산 결과를 재료 물성치를 이용한 등가 음향임피던스 산정 결과와 비교·검토하였고, 이들 결과 간 최대 차이는 약 0.7 dB로써 상호 부합성이 높음을 확인하였다.

따라서, 이 연구에서 활용한 임의 재질 평판의 등가 음향임피던스 역산 방법은 수중함 선체에 부착되는 음향 타일, 흡음재 등과 같은 재료의 등가 음향임피던스 평가에 유용하게 활용될 수 있을 것으로 판단한다. 향후에는 음장 규모가 큰 잔향수조, 예인 수조 등에서 동일한 실험을 수행하여 수중 평판에 의한 산란, 회절 등의 영향성과 구면파의 평면파 가정을 만족하는 실험 설계 등에 관한 추가적인 연구를 수행하고자 한다.

Acknowledgments

이 논문은 조선해양플랜트글로벌핵심연구센터의 관리 하에 2024년도 정부(방위사업청)의 재원으로 국방기술진흥연구소의 지원을 받아 수행된 연구임(No. KRIT-CT-23-018, 잠수함 첨단함형 특화연구실).

References

• Audoly, C. and Giangreco, C., 1991, Global Characterization of Multilayer Panels for Underwater Applications, Journal of Wave-material Interaction, Vol. 5, No. 1, pp. 55~72.
• Piquette, J. C. and Forsythe, S. E., 2001, Low-frequency Echo-reduction and Insertion-loss Measurements from Small Passive-material Samples under Ocean Environmental Temperatures and Hydrostatic Pressures, Journal of the Acoustical Society of America, Vol. 110, No. 4, pp. 1998~2006. [https://doi.org/10.1121/1.1402115]
• Shin, M.-R., Cho, J.-H., Lee, K.-T., Kim, J.-S. and Jeon, J.-J. et al., 2011, Measurement System for Performance Evaluation of Acoustic Materials in a Small Water Tank, Journal of the Acoustical Society of Korea, Vol. 30, No. 2, pp. 63~72. [https://doi.org/10.7776/ASK.2011.30.2.063]
• Jung, W.-J., Han, S.-J., Kim, W.-H., Shin, K.-K. and Jeon, J.-J., 2006, A Study on the Measurement and Analysis Method for the Acoustic Transmission Loss of the Material for the Acoustic Window of Sonar Dome, Transactions of the Korean Society for Noise and Vibration Engineering, Vol. 16, No. 7, pp. 729~738. [https://doi.org/10.5050/KSNVN.2006.16.7.729]
• Gartland, G. J., Radcliffe, C. J. and Hull, A. J., 2009, Measurement of Dilatational Wave Speed using an Echo Reduction Test, Journal of Sound and Vibration, Vol. 320, No. 3, pp. 491~495. [https://doi.org/10.1016/j.jsv.2008.12.004]
• Ko, S. H., Pyo, S. W. and Seong, W. J., 2001, Structure-borne and Flow Noise Reductions: Mathematical Modeling, Seoul National University Press, Seoul, Korea.
• Knott, E. F., Shaeffer, J. F. and Tuley, M. T., 1993, Radar Cross Section, 2nd Edition, Artech House, Boston, United States.
• Kinsler, L. E., Frey, A. R., Coppens, A. B. and Sanders, J. V., 2000, Fundamentals of Acoustics, 4th Edition, John Wiley & Sons, NY, United States.
• Lee, J.-Y., Kim, K., Park, S.-J. and Cho, D.-S., 2024, Experimental Validation on Underwater Sound Speed Measurement Method using Cross-correlation of Time-domain Acoustic Signals in a Reverberant Water Tank, Journal of the Society of Naval Architects of Korea, Vol. 61, No. 1, pp. 1~7. [https://doi.org/10.3744/SNAK.2024.61.1.1]
• Abdel-Wahab, A. A., Ataya, S. and Silberschmidt, V. V., 2017, Temperature-dependent Mechanical Behaviour of PMMA: Experimental Analysis and Modelling, Polymer Testing, Vol. 58, pp. 86~95. [https://doi.org/10.1016/j.polymertesting.2016.12.016]