오목 멤브레인의 저차 고유치 미 추출 문제 극복을 위한 분할 영역법 기반 무차원동영향함수법 개발: 제1부(이론 정립과 검증)

2.1 두 영역 분할법(Two-domain Method)

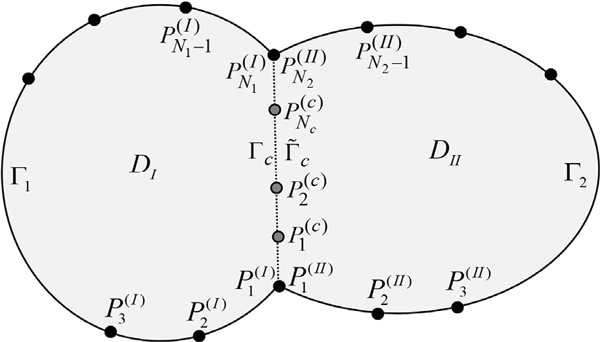
오목 형상 멤브레인의 고정밀도 고유치 해석을 위해 개발된 영역 분할법 기반 무차원동영향함수법은 Fig. 1과 같이 오목 형상 멤브레인을 여러 개의 볼록 형상 영역으로 분할하는 데서 출발한다. 이 논문에서는 오목 멤브레인을 2개의 영역 D_I과 D_II로 분할한 두 영역 분할법만을 다루며, 3개 이상의 영역으로 분할하는 다 영역 분할법(multi-domain method)은 이 논문의 2부에서 고려된다.

Fig. 1

Concave membrane divided into two domains DI and DII

Fig. 1과 같이 볼록 영역 D_I은 외부 경계 Г₁과 D_II와의 접경로 둘러싸여 있다. 경계 Г₁은 N₁개의 절점 $$ P_1^{\left(I\right)},P_2^{\left(I\right)},\cdots ,P_{N1}^{\left(I\right)}$$로 이산화되고, 경계는 N_c개의 절점 $$ P_1^{\left(C\right)},P_2^{\left(C\right)},\cdots ,P_{Nc}^{\left(C\right)}$$로 이산화된다. 볼록 영역 D_II는 외부 경계 Г₂와 접경 Г_c로 둘러싸여 있으며 외부 경계 Г₂는 N₂개의 절점 $$ P_1^{\left(II\right)},P_2^{\left(II\right)},\cdots ,P_{N2}^{\left(II\right)}$$로 이산화된다.

2.2 분할된 영역 내부 변위 가정

영역 D_I의 내부 변위 W_I(r)은 경계 Г₁과 Г_c 상의 절점에서 정의된 무차원 동영향 함수들의 선형결합⁽¹⁾으로 식 (1)과 같이 가정한다.

여기서 Λ는 주파수 파라미터, r은 영역 D_I에 위치한 한 점에 대한 위치 벡터를 의미하며, J₀(⋯)는 제1종 0차 베셀함수(Bessel function)로 주어지는 멤브레인의 무차원 동영향 함수이다. 그리고 $$ {\mathbf{r}}_i^{\left(1\right)}$$와 $$ {\mathbf{r}}_k^{\left(c\right)}$$는 경계 Г₁에 위치한 i번째 절점에 대한 위치벡터와 접경 Г_a에 위치한 k번째 절점에 대한 위치벡터를 각각 나타낸다. 또한, $$ A_i^{\left(1\right)}$$와 $$ A_k^{\left(c\right)}$$는 경계 Г₁에 위치한 i번째 절점에 정의된 베셀 함수 J₀의 기여도와 접경 Г_a에 위치한 k번째 절점에 정의된 베셀 함수 J₀의 기여도를 각각 의미한다.

영역 D_I과 마찬가지 방식으로, 영역 D_II의 내부 변위 W_II (r)는 경계 Г₂와 Г_c 상의 절점에서 정의된 무차원 동영향 함수들의 선형결합⁽¹⁾으로 식 (2)와 같이 가정한다.

여기서 r은 영역 D_II에 위치한 한 점에 대한 위치 벡터를 의미한다. 그리고 $$ {\mathbf{r}}_j^{\left(2\right)}$$는 경계 Г₂에 위치한 j번째 절점에 대한 위치벡터를 나타낸다. 또한, $$ B_j^{\left(2\right)}$$와 $$ B_k^{\left(c\right)}$$는 경계 Г₂에 위치한 j번째 절점에 정의된 베셀 함수 J₀의 기여도와 접경에 위치한 k번째 절점에 정의된 베셀 함수 J₀의 기여도를 각각 의미한다.

2.3 글로벌 시스템 행렬식 구성

해석 대상 멤브레인이 고정단 경계(fixed boundary)를 가지므로, 외부 경계 Г₁과 Г₂에서 변위가 0인 경계 조건을 고려하면 식 (3), 식 (4)와 같은 로컬 시스템 행렬식을 각각 얻을 수 있다⁽¹⁾.

여기서 시스템 행렬 SM₁₁, SM_1c, SM₂₂, SM_2c와 벡터 A₁, A_c, B2, B_c의 성분은 이전 논문에서⁽¹⁾ 확인 가능하기에 지면 관계상 설명을 생략한다.

다음으로 접경 Г_c에서의 변위와 기울기 연속 조건을 고려하면 식 (5)와 식 (6)과 같은 로컬 시스템 행렬식을 각각 얻을 수 있다⁽¹⁾.

여기서 시스템 행렬들의 성분은 이전 논문에서 확인 가능하다⁽¹⁾.

4개의 로컬 시스템 행렬식 식 (3) ~ 식 (6)으로부터 하나의 글로벌 시스템 행렬식을 추출하기 위해, 우선 식 (3)과 식 (4)를 식 (7) 및 식 (8)과 같이 각각 변형한다.

식 (7)과 식 (8)을 식 (5)와 식 (6)에 대입하면 식 (9)와 같은 하나의 글로벌 시스템 행렬식이 구해진다.

여기서 주파수 파라미터 Λ의 함수인 글로벌 시스템 행렬 SM(Λ)와 기여도 벡터 C는 식 (10) 및 식 (11)과 같다.

식 (9)로부터 멤브레인의 고유치는 글로벌 시스템 행렬의 판별식이 0이 되는 조건 식 (12)로부터 구할 수 있다.

3.1 저차 고유치 미 추출 문제 규명

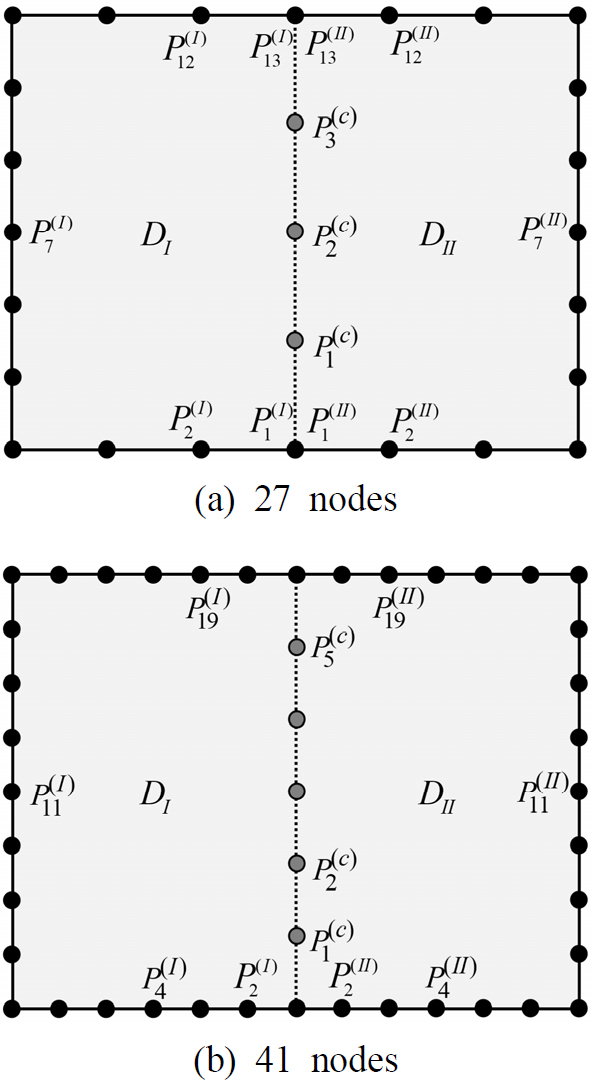
이전 연구에서 무차원동영향함수법은 절점이 증가하면 저차 고유치들이 미 추출되는 현상이 확인되었다^(4~6). 이러한 현상이 분할영역법 기반 무차원동영향함수법에도 나타나는 지 확인하고 그 해결책을 찾기 위해 엄밀해가 존재하는 직사각형 멤브레인(가로 1.2 m, 세로 0.9 m)을 Fig. 2와 같이 두 개의 영역 D_I과 D_II로 분할하였다. Fig. 2(a)는 외부 경계에 24개 절점과 접경에 3개 절점으로 총 27개 절점으로 이산화한 경우이다. Fig. 2(b)는 외부 경계에 36개 절점과 접경에 5개 절점으로 총 41개 절점으로 이산화한 경우이다.

Fig. 2

Rectangular membranes divided into two domains and discretized with 27 and 41 nodes, respectively

Fig. 3의 실선은 27개 절점으로 이산화한 멤브레인(Fig. 2(a))에 대한 판별식 곡선을 식 (13)을 이용하여 그린 결과이다⁽⁴⁾.

Fig. 3

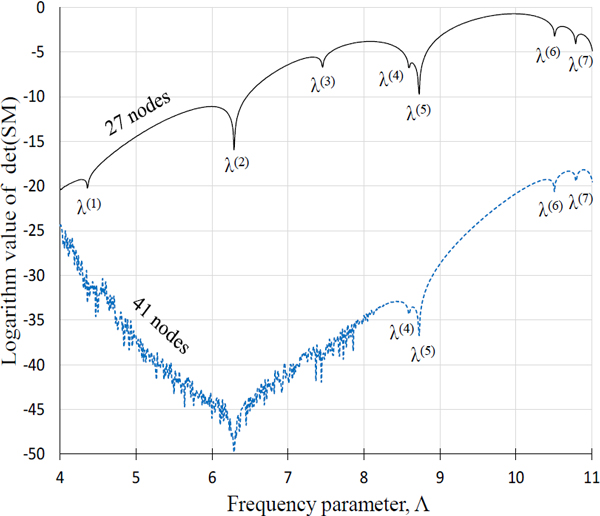
Determinant curves of the rectangular membrane for 27 and 41 nodes plotted by the previous NDIF method using Eq. (13) or Eq. (14)

여기서 S는 시스템 행렬 SM(Λ)의 크기이며 접경 절점 개수의 두 배인 S = 6이며, γ_k(Λ)는 시스템 행렬 SM(Λ)에 대한 대수 고유치 문제에서의 k번째 고유치를 의미한다⁽⁴⁾. 이 곡선에서 극소값에 해당되는 주파수 파라미터 값들이 고유치에 해당된다. 이 고유치들은 Table 1에 정리되었다. 이 고유치들을 엄밀해(exact solution)와 비교해보면, 저차(1차 ~ 5차) 고유치들은 정확히 일치하나 고차(6차, 7차) 고유치들이 약간의 오차가 있음이 보인다. 그래서 Fig. 2(b)와 같이 절점 수를 27개에서 41개로 증가시킨 후 식 (13)을 이용하여 판별식 곡선을 그렸으며 그 결과는 Fig. 3의 점선 곡선에 해당된다. 이때 시스템 행렬의 크기는 접경 절점 개수의 두 배인 S = 10이다. 점선 판별식 곡선을 살펴 보면, 저주파수 영역에서는 시스템 행렬이 발산하여 저차(1차 ~ 3차)의 고유치가 추출되지 않고, 고차(4차 ~ 7차) 고유치만이 추출되었음을 알 수 있다. 점선 판별식 곡선으로부터 추출한 고유치들은 Table 1에 요약되었다. 절점 수가 증가했기 때문에 고차(6차, 7차) 고유치들이 엄밀해와 정확히 일치했음을 Table 1에서 확인 가능하다⁽⁷⁾. 그러나 저차(1차 ~ 3차) 고유치들이 추출되지 않는 문제점이 발견된다.

Table 1

Eigenvalues of the rectangular membrane obtained by the previous NDIF method using Eq. (13) or Eq. (14), the exact solution and FEM(ANSYS)

3.2 저차 고유치 미 추출 문제 해결 방안

Fig. 3의 점선 판별식 곡선에서 저차 고유치가 추출되지 않는 이유는 접경 절점 수가 증가하여 저주파수 영역에서 시스템 행렬이 발산(기저함수가 서로 독립적이지 않기 때문에 발산)하기 때문인 것으로 추정되며, 이러한 발산 현상 때문에 시스템 행렬의 판별식 값이 왜곡되어 계산되게 된다⁽⁴⁾. 시스템 행렬의 판별식 값을 정확히 구하기 위해서는 시스템 행렬의 랭크(rank)를 이용하는 식 (14)와 같은 판별식 값 계산 방법이 필요하다^(4~6).

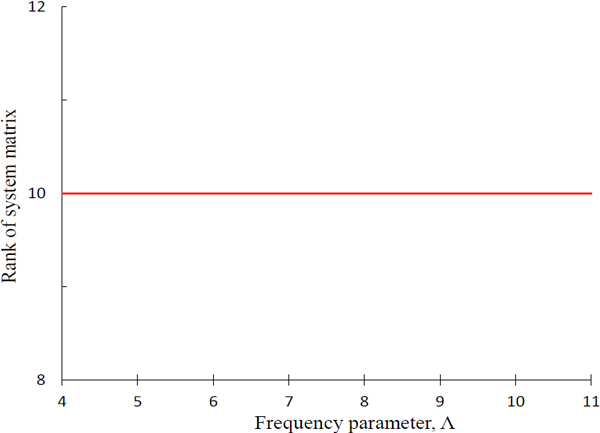
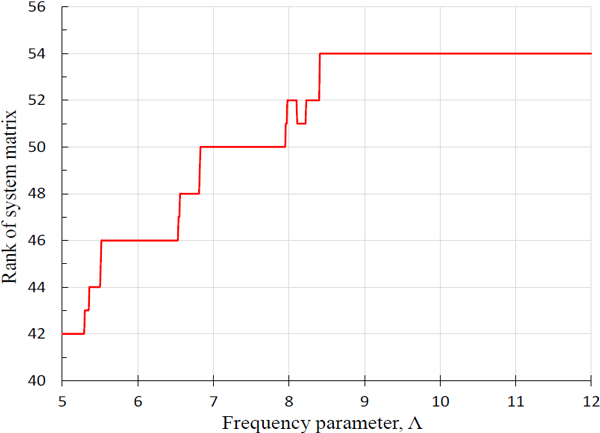
여기서 R(Λ)는 시스템 행렬의 랭크이다. 41개 절점으로 이산화한 경우에 대한 시스템 행렬의 랭크 R(Λ)을 주파수 파라미터 Λ의 함수로 Fig. 4와 같이 계산하였다. Fig. 4를 살펴보면, 시스템 행렬의 랭크의 크기가 전체 주파수 대역에서 10으로 시스템 행렬의 크기와 같은 일정한 값을 가진다. 즉, R(Λ) = S가 성립하여 식 (14)가 식 (13)과 같아지게 되어 식 (14)의 유효성이 사라지게 된다. 결과적으로, 식 (14)를 이용하여 판별식 곡선을 그리더라도 Fig. 3의 곡선과 같은 결과가 나오는 문제점이 발생하게 된다.

Fig. 4

Rank of SM for the rectangular membrane discretized with 41 nodes

R(Λ) = S이 된 이유를 알아 내기 위해 식 (10)으로 주어진 글로벌 시스템 행렬의 성분을 살펴보고자 한다. 분할영역법을 사용하지 않은 이전 연구에서 식 (10)의 성분에 포함된 SM₁₁과 SM₂₂발산이 시스템 행렬의 랭크를 시스템 행렬의 크기보다 작게 만드는 원인으로 분석되었다. 그런데 식 (10)에서는 SM₁₁과 SM₂₂가 역행렬의 형태인 $$ {\mathbf{S}\mathbf{M}}_{11}^{-1}$$과 $$ {\mathbf{S}\mathbf{M}}_{22}^{-1}$$로 변환되었기 때문에 글로벌 시스템 행렬이 발산하지 않아 R(Λ) = S이 된 것으로 분석된다. 그래서 이 논문에서는 SM₁₁과 SM₂₂이 역행렬 변환없이 시스템 행렬의 성분에 그대로 포함되도록 새로운 방식의 글로벌 시스템 행렬 추출 방안을 제안한다

$$ {\mathbf{S}\mathbf{M}}_{11}^{-1}$$과 $$ {\mathbf{S}\mathbf{M}}_{22}^{-1}$$은 식 (7), 식 (8)과 같이 미지 기여도 벡터 A₁과 A₂를 소거하여 시스템 행렬을 축약하는 과정에서 생성되므로, 축약 과정 없이 글로벌 시스템 행렬을 추출하고자 한다. 4개의 로컬 시스템 행렬식 식 (3) ~ 식 (6)은 식 (15)와 같이 하나의 행렬식으로 표현이 가능하다.

여기서 TM(Λ)와 D는 새로이 추출된 시스템 행렬과 기여도 벡터로 식 (16) 및 식 (17)과 같이 각각 구해진다.

여기서 TM(Λ)의 크기는 S = 48이다. 왜냐하면 Fig. 2(b)에서와 같이 영역 D_I과 D_II를 둘러싸고 있는 절점 수가 둘 다 24개이고 이 두 값의 합에 해당되는 값인 48이 TM(Λ)의 크기가 되기 때문이다. 식 (16)의 시스템 행렬을 식 (14)에 대입하면 식 (18)과 같다.

여기서 R_T(Λ)는 시스템 행렬 TM의 랭크, τ_k(Λ)는 시스템 행렬 TM에 대한 대수 고유치 문제⁽⁴⁾에서의 k번째 고유치를 의미한다.

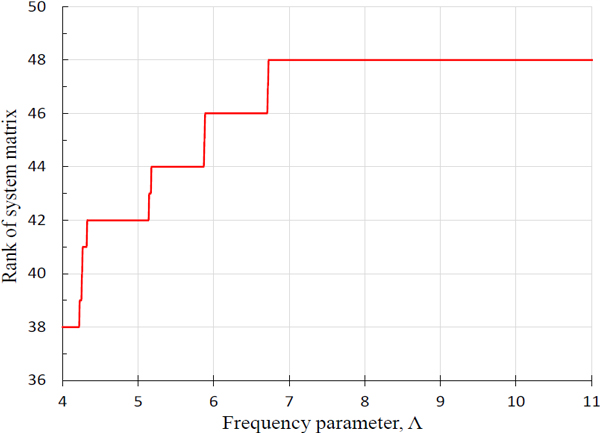
앞에서 설명한 바와 같이 식 (18)이 유효성을 갖기 위해선 랭크 R_T(Λ)이 시스템 행렬이 발산하는 주파수 영역에서 시스템 행렬의 크기 S보다 작은 값을 가져야 한다. 이를 확인하기 위해 TM의 랭크 곡선을 그리면 Fig. 5와 같다. 이 랭크 곡선이 저주파수 영역에서 R_T(Λ) < S을 만족함을 확인할 수 있다.

Fig. 5

Rank of TM for the rectangular membrane discretized with 41 nodes

식 (18)을 이용하여 판별식 곡선을 그린 후 불연속성을 제거하는 과정⁽⁴⁾을 거치면 Fig. 6과 같은 판별식 곡선이 그려진다. 이 판별식 곡선은 Fig. 3의 점선 판별식 곡선과는 달리 저주파수 영역에서 판별식 값이 발산하는 문제점이 사라졌음을 확인할 수 있다. Fig. 6의 곡선으로부터 추출한 고유치는 Table 2에 요약하였다⁽⁷⁾. Table 2에서 식 (18)에 의해 구한 고유치들과 엄밀해가 정확히 일치함을 확인할 수 있으며, 이를 통해 이 논문에서 제안된 식 (18)이 정확한 고유치 추출을 보장한다고 말할 수 있다. 다음 절에서는 오목한 홈을 가진 임의 형상 오목 멤브레인에 대해 식 (18)의 타당성과 정확성을 검증하고자 한다.

Fig. 6

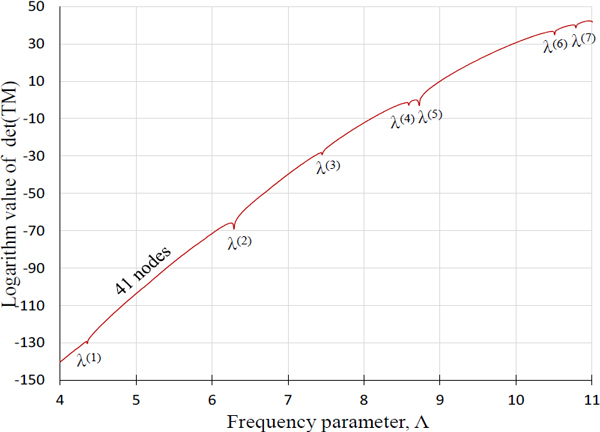
Determinant curve of the rectangular membrane for 41 nodes plotted by the proposed method using Eq. (18)

Table 2

Eigenvalues of the rectangular membrane for 41 nodes plotted by the proposed method using Eq. (18) and the exact solution

3.3 임의 형상 오목 멤브레인 예제 검증

이 논문에서 제안된 식 (18)이 Fig. 7과 같은 깊은 홈을가진 임의 형상 오목 멤브레인에 대해서도 타당한 지를 확인하고자 한다. Fig. 7(a), Fig. 7(b)와 같이 오목 멤브레인을 두 개의 볼록 영역으로 나눈 후 각각 30개와 49개의 절점으로 이산화 하였다. 먼저 30개 절점으로 이산화한 멤브레인에 식 (13) 또는 식 (14)를 이용한 기존 무차원동영향함수법을 적용하면 Fig. 8의 실선 판별식 곡선을 얻을 수 있다. 이 판별식 곡선의 극소값에 해당하는 1차 ~ 8차 고유치들은 Table 3에 요약되었다. 이들 고유치들을 1701개 절점을 사용한 FEM 고유치들과 비교해보면, 약간의 오차만을 가짐을 확인할 수 있다. FEM과 마찬가지로 무차원동영향함수법 또한 절점의 개수를 증가시키면 해의 정밀도가 올라가므로, Fig. 7(b)와 같이 절점의 수를 30개에서 49개로 증가시킨 후 식 (13) 또는 식 (14)를 이용해 판별식 곡선을 그리면 Fig. 8의 점선 곡선이 된다. 이 점선 곡선을 살펴보면, 주파수 파리미터 값이 11이하인 저주파수 영역에서 시스템 행렬이 발산하여, 단지 6차 ~ 8차 고유치만이 추출되는 문제점을 확인할 수 있다. 추출된 3개의 고차 고유치들은 Table 3에 요약되었으며, 이 고유치들은 1701개를 사용한 FEM 결과에 더 근접했음을 알 수 있다.

Fig. 7

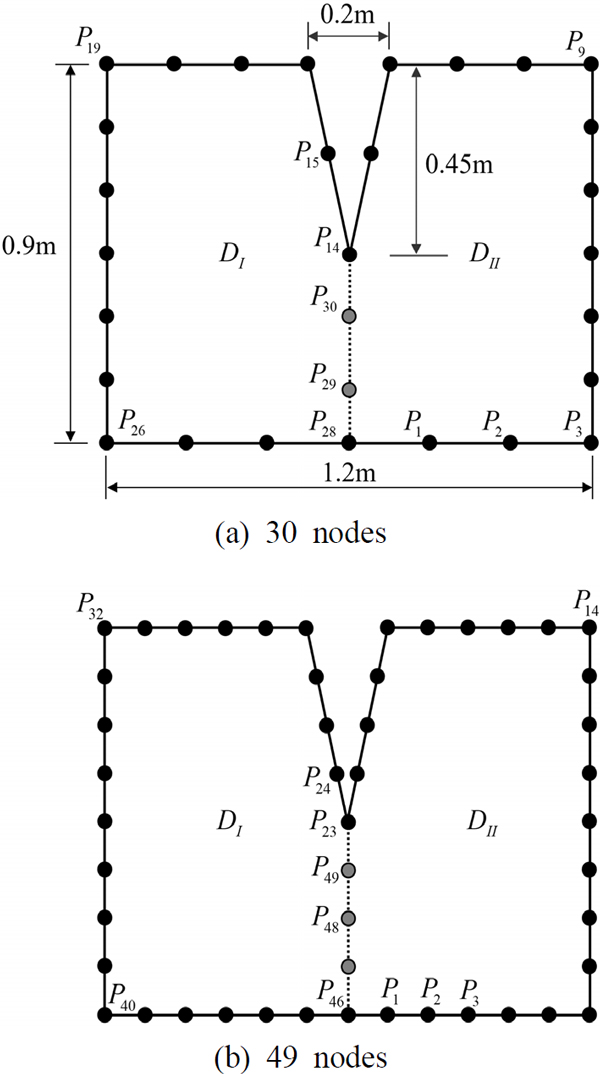
Highly concave membranes divided into two domains and discretized with 30 and 49 nodes, respectively

Table 3

Eigenvalues of the highly concave membrane obtained by the previous NDIF method using Eq. (13) or Eq. (14), FEM(ANSYS) and the proposed method

Fig. 8

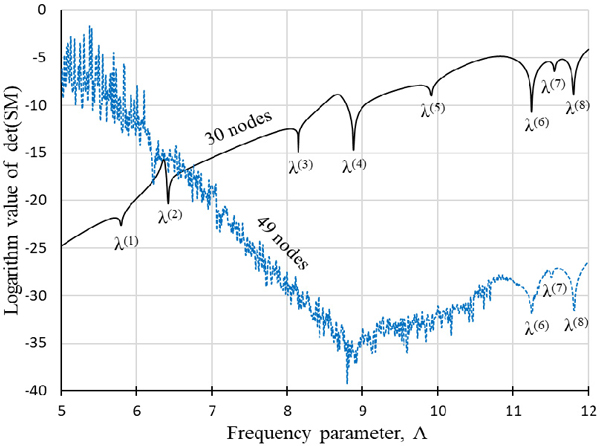
Determinant curves of the highly concave membrane for 30 and 49 nodes plotted by the previous NDIF method using Eq. (13) or Eq. (14)

상기의 저차 고유치 미 추출 문제를 해결하기 위해 이 논문에서 제안된 식 (18)을 사용하여 Fig. 9와 같은 판별식 곡선을 그렸다. 식 (18)을 계산하기 위해 사용된 시스템 행렬의 랭크 곡선은 Fig. 10과 같다. 이 판별식 곡선을 살펴보면 모든 주파수 영역에서 시스템 행렬이 발산하지 않음을 확인할 수 있으며, 결과적으로 1차 ~ 8차 고유치 모두가 성공적으로 추출되었음도 확인된다. 이들 고유치들은 Table 3의 마지막 열에 정리되었으며, FEM 보다 훨씬 적은 절점을 사용했음에도 FEM 고유치에 거의 근접함도 확인된다.

Fig. 9

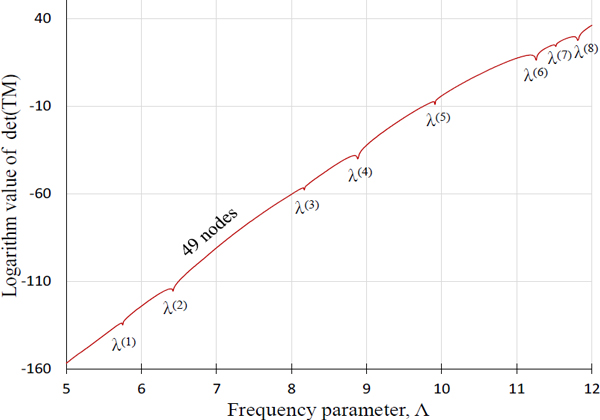
Determinant curve of the highly concave membrane for 49 nodes plotted by the proposed method using Eq. (18)

Fig. 10

Rank of TM for the highly concave membrane discretized with 49 nodes