상태감시 데이터 및 디지털 트윈 모델을 이용한 추진축계 건전성 및 수명예측 기법 개발

1. 서 론

최근 효율적인 함정 운용을 위해서 상태감시시스템을 함정의 주요장비에 설치하고 이 데이터를 이용한 상태기반정비(condition based maintenance) 뿐만 아니라 상태기반 예지 정비(condition based maintenance plus)를 효과적으로 수행하기 위한 많은 연구가 이루어지고 있다. 하지만 국내 해군의 경우 통합기관제어체계인 ICAS(interactive collection analysis system)를 이용한 상태기반 정비를 지향하고 있으나 ICAS 시스템의 경우 국외 도입 시스템으로 상태감시 데이터의 활용 및 센서 추가로 인한 상태 데이터 확보 등 효과적 활용을 위한 조치를 취하지 못하고 있는 실정이다. 따라서 최근 국내 기술로 통합기관제어체계 개발이 완료되었으며 신규 개발되는 함정에 탑재될 예정임에 따라 국내 함정의 상태기반 정비에 대한 발전이 기대되고 있다.

개발 및 운용함정 추진축의 경우 품질문제가 가장 많이 발생하는 요소 중 하나이므로 상태감시장치를 이용하여 추진축계의 건전성을 모니터링하고 주요 이벤트 발생 시 이에 대한 평가가 필요하며 통합기관제어체계와 연계하여 운용되어야만 한다.

이러한 실시간 모니터링을 통해 얻어진 데이터를 기반으로 대상 시스템의 고장분석을 효과적으로 수행하기 위해 최근 디지털 트윈 적용에 대한 검토가 활발히 이루어지고 있다.

Oh는 구조물에 대한 디지털 트윈 모델을 구현하여 실제 계측 없이 디지털 트윈 모델을 이용하여 구조물의 진동상태를 파악하는 연구를 수행하였다⁽¹⁾.

Hwang은 제조 컨베이어 시스템을 Arena 시뮬 레이션 모델을 통해 개발하여 효율적인 생산 라인 운용을 위한 디지털 트윈을 제안하였다⁽²⁾. Heron은 군용무인차량의 디젤엔진의 주요고장모드인 연료가스 누설 등을 실시간으로 파악하기 위해서 상태감시시스템 센서 및 디지털 트윈을 이용하였으며 오토엔코더 뉴럴네트워크(autoencoder neural network) 알고리즘을 이용한 고장판단 알고리즘을 제안하였다⁽³⁾. 조선, 해양분야에서도 이러한 상태감시 센서를 통해 얻어진 상태 데이터를 입력으로 하는 다양한 디지털 트윈 적용에 대한 연구가 활발히 이루어지고 있다^(4~7).

이 연구에서는 정상 운전중 과도 하중 발생뿐만 아니라 비정상적인 충격 하중 발생 이벤트까지 고려한 추진축계의 상대감시 및 건전성 평가 모니터링 시스템을 제안하고자 한다. 따라서 추진축에 작용하는 하중을 정상상태 및 비정상상태로 분류하여 축이 받는 스트레스에 대한 축의 손상도를 계산하였다. 정상상태일 경우 일반적인 항해 중 항해조건의 변화로 작동하중이 증가하였을 때 축에 가해지는 손상에 대해 고장분석 및 평가 알고리즘을 통해 평가하고, 비정상상태의 경우 함정 운용 시 외부 부유물 충돌 등 추진축에 비정상적으로 발생하는 충격하중에 대해 디지털 트윈을 이용하여 추진축계 건전성을 평가하는 방안을 제안하고자 한다.

2. 추진축계 디지털 트윈 모델

디지털 트윈은 물리적 물체를 정확하게 반영하도록 컴퓨터상에 가상모델을 만들고 현실에서 발생할수 있는 상태를 센서 네트워크를 통해 계측하여 이를 기반으로 가상모델을 시뮬레이션 하는 기술을 말한다.

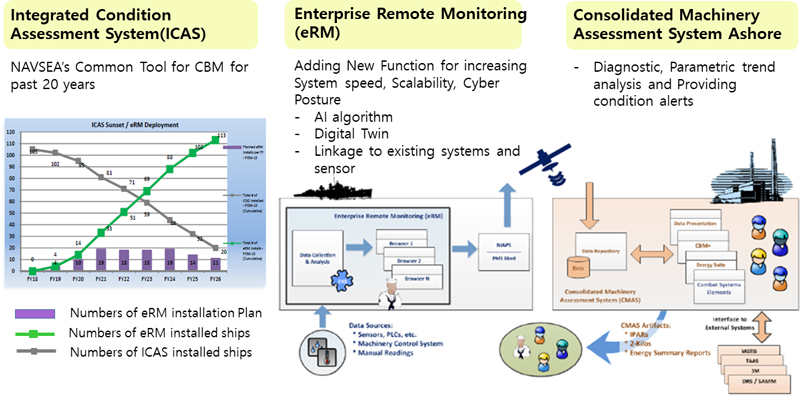
미해군의 경우 추진체계의 상태감시를 위해 통합기관추진체계로 ICAS(interactive collection analysis system)를 사용하고 있다. 하지만 ICAS를 가지고 고장에 대한 경보는 가능하나 현재 장비의 상태를 진단하고 수명을 예측하여 정비주기를 결정하는 예지정비를 수행하지 못함에 따라, 최근에는 Fig. 1과 같이 eRM(enterprise remote control) 개념을 도입한 ICAS with eRM 시스템이 장착되고 있다⁽⁸⁾.

Fig. 1

Conceptual diagram of the ICAS with eRM in US navy

Fig. 1과 같이 ICAS with eRM 시스템은 ICAS를 이용하여 추진체계의 상태데이터를 군위성을 통해 실시간으로 육상종합기계시스템으로 송부하여 분석하고 그 결과를 다시 함정으로 피드백하는 개념의 시스템이다.

ICAS의 상태감시데이터가 육상종합기계시스템으로 전송되면 이 데이터를 가지고 디지털 트윈을 통해 주요장비, 체계의 손상도를 계산하고 그 결과를 가지고 AI 알고리즘 등을 통해 고장발생 및 수명을 예측하여 정비함으로써 상태기반예지정비(condition based maintenance plus)의 목적을 달성할 수 있다.

이 연구에서는 이러한 미해군의 ICAS with eRM 시스템을 참고하여 국내 함정의 추진축계의 건전성을감시하고 이를 기반으로 예지정비를 수행하기 위한 디지털 트윈 모델을 개발하고자 한다.

일반적으로 정상 운전 상태에서의 축에 작용하는 힘에 대한 응력은 해석 및 실선 시운전 진동 시험을 통해서 각 속도별 최대응력지점 및 응력값을 파악할 수 있으며 항해조건에 따라 입력하중이 증가했을 경우 최대응력은 선형적으로 증가한다고 가정할 수 있다. 따라서 상태감시시스템을 통해서 추진축에 작용하는 하중을 모니터링하면 최대응력 발생위치와 응력값은 예측이 가능하다. 따라서 정상 운전 상태에서는 상태감시 시스템만 가지고도 추진축의 건전성 평가가 가능하므로 디지털 트윈의 적용은 필요하지 않다.

하지만 충격하중과 같이 비정상 상태의 하중이 추진축에 발생할 경우 충격하중의 방향과 충격하중의 지속시간의 경우의 수가 무한하기 때문에 해석 및 실선 시운전 시험을 수행하기 어렵다. 따라서 충격력을 계측하는 상태감시 시스템을 가지고 비정상 운전조건에서 충격력을 계측한다 하더라도 최대응력점과 최대응력값을 파악하기는 어렵다.

따라서 이 경우 충격력을 상태감시시스템으로 계측하고 이를 입력으로 디지털 트윈 모델을 해석하면 최대응력점과 최대응력값을 예측할 수 있으므로 디지털 트윈 적용으로 축의 건전성을 평가할 수 있다.

따라서 이 절에서는 비정상 운전조건인 충격하중 발생 시 축의 건전성을 평가하기 위한 디지털 트윈에 대해서 다루고자 하며 이를 위해 한국해군에서 운용하고 있는 특정 함정의 추진축에 대해서 디지털 트윈 모델을 개발하고자 한다.

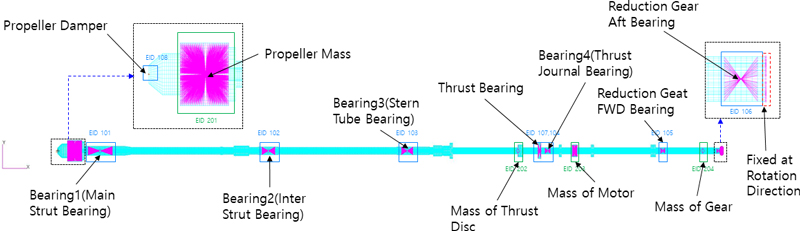
Fig. 2는 이 연구에서 다루는 추진축계에 대한 디지털 트윈 모델이다.

Fig. 2

FEM model of the propulsion shaft for a particular naval vessel in this research

Fig. 2의 디지털 트윈 모델은 MSC. Patran을 이용하여 유한요소(FEM) 모델로 정의하였다. Fig. 2의 추진축의 경우 감속기어가 강체지지로 선체에 부착되어 있어 감속기어 연결축은 고정단으로 처리할수 있으므로 추진축계 모델은 프로펠러부터 감속기어 입구 축까지만 고려하여 모델링 하였다.

추진축의 경우 육면체 요소(hexa element)를 적용하여 모델링하였으며 추진축의 재질은 강재로 밀도, 영률 및 푸아송비는 강재의 값을 사용하였다(ρ = 7850 kg/m³, E = 2.11e¹¹ N/m², ν = 0.3).

프로펠러 질량의 경우 부가수질량을 고려하여 집중질량으로 모델링하였으며 추력베어링 디스크 질량, 추진전동기 로터의 질량, 감속기어의 질량도 각각 집중질량으로 0D 절점요소(point element) 및 RBE3 요소를 사용하여 모델링하였다. 베어링의 경우 0 bush 요소를 사용하여 모델링 하였으며 추력베어링은 축방향에 대해서만 강성과 감쇠를 적용하였고 나머지 베어링의 경우 저널베어링으로 수평, 수직방향에 대해서만 강성 및 감쇠를 적용하였다.

프로펠러의 경우 일반적으로 유체감쇠가 적용되는데 이는 프로펠러에 0 bush 요소를 사용하여 수직, 수평, 축방향에 대해 감쇠를 적용하였다.

추진축계 질량 및 베어링 요소에 대한 물성치는 Table 1, Table 2와 같다.

Table 1

Properties of mass

Table 2

Properties of bearings

3. 디지털 트윈 모델 해석을 통한 충격하중의 정의

추진축계의 충격하중을 계측하기 위해서 상태감시 센서는 다음과 같이 구성하였다.

(1) 축방향 충격력 : 추력베어링 부착 포스트랜스듀서(force transducer) 또는 추력베어링 하우징 부착 축방향 가속도계.

(2) 횡방향 충격력 : 주스트러트(main strut) 베어링 부착 포스트팬스듀서(force transducer) 또는 추력베어링 하우징 부착 수직, 수평방향 가속도 센서.

(3) 비틀림 충격토크 : 감속기어 출력축 부착 스트레인게이지 또는 토크센서.

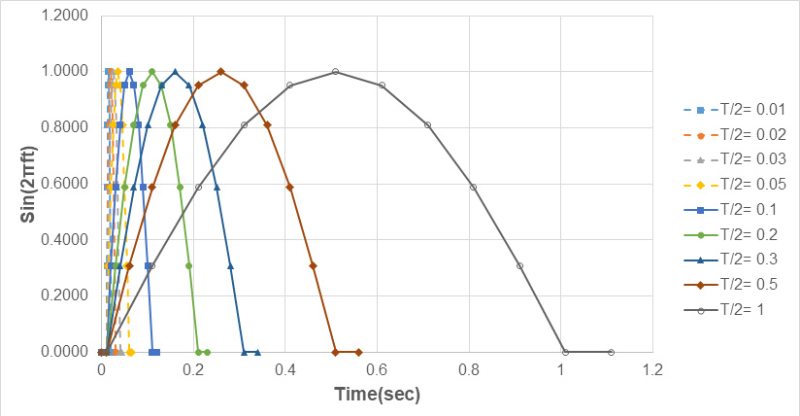
외부 충격력은 프로펠러에서만 발생한다고 가정하여 프로펠러에 가해지는 충격력의 형태는 Fig. 3과 같이 반사인파(half sine wave)로 가정하였다. 해석은 같은 크기의 충격력에 대해 지속시간만 달리하여 각 방향별로 해석하였다.

Fig. 3

Shock profile on the propeller(half sine wave)

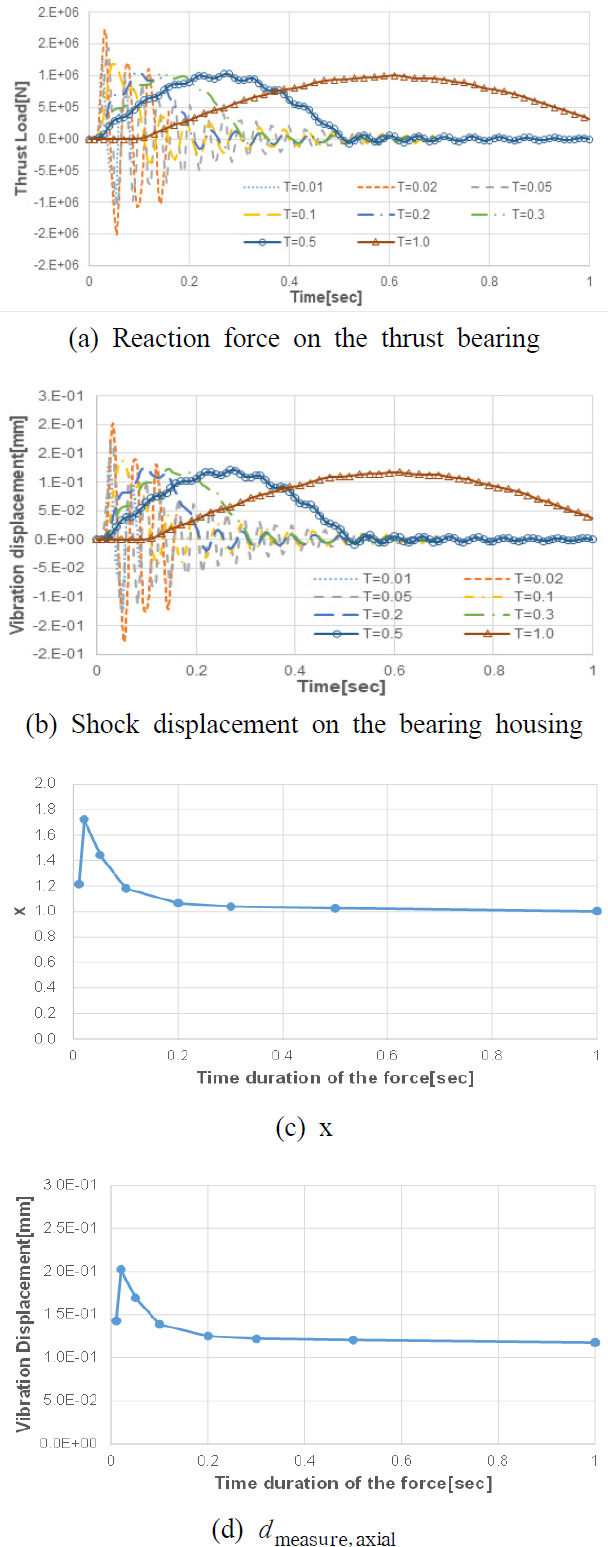
축방향의 경우 Fig. 4와 같이 추력베어링의 축방형 반력 및 추력베어링 하우징에서 계산된 가속도의 크기와 프로펠러에 입력한 충격력의 크기와의 관계를 충격지속시간에 따라 각각 구하였다.

Fig. 4

Thrust shock and resultant bearing reaction force(thrust bearing) and displacement

이러한 해석 결과를 기반으로 상태감시시스템으로부터 충격 발생 시 충격지속시간과 추력베어링의 충격 반력 크기 및 베어링에서의 가속도를 계측하면 프로펠러에 작용한 축방향 힘을 식 (1), 식 (2)와 같이 정의할 수 있다.

여기서 F_pp,axial은 프로펠러에 작용하는 축방향 충격하중, F_{thrust,measure}는 추력베어링에 부착한 포스트랜스듀서에서 계측한 베어링 반력, F_{thrust,1000 kN}은 충격해석으로부터 1000 kN 프로펠러 축방향 충격력에 대한 추력베어링에서의 반력 해석 결과, d_{measure,axial}은 추력베어링 하우징에서 계측한 축방향 충격 변위, d_{1000 kN,axial}은 충격해석을 통해 추력베어링 하우징에서의 축방향 충격 변위 해석결과이다.

Fig. 5는 충격지속시간 0.01초, 0.02초, 0.05초, 0.1초, 0.2초, 0.3초, 0.5초, 1.0초에 대해 프로펠러에 축방향 하중 10⁶ N 인가 시 추력베어링 반력 및 축방향 진동변위 응답 해석결과이다. Fig. 5로부터 식 (1), 식 (2)의 x 및 d_1000kN을 구할수 있으며 상태감시 데이터를 통해서 얻어진 추력베어링 반력 및 진동변위를 가지고 축방향 충격하중을 정의할 수 있다.

Fig. 5

Reaction force and shock displacement on the thrust bearing housing for the axial shock

굽힘방향의 경우 Fig. 6과 같이 프로펠러에 입력으로 가한 충격력의 크기와 주스트러트(main strut) 베어링에서 계산한 베어링 반력 및 추력베어링 하우징에서 계산한 굽힘방향 가속도의 크기와의 관계를 충격지속시간에 따라 각각 구하였다. 따라서 상태감시시스템으로부터 충격 발생 시 충격지속시간과 주스트러트(main strut) 베어링 반력 및 추력베어링에서의 가속도 크기를 계측하면 프로펠러에 작용한 축방향 힘을 식 (3), 식 (4)와 같이 정의할 수 있다.

Fig. 6

Shock in the bending direction and resultant bearing(main strut bearing) reaction force and displacement

여기서 F_pp,bending은 프로펠러에 작용하는 굽힘방향 충격하중, F_MS,bearing은 주스트러트 베어링의 포스트랜스듀서에서 계측한 베어링 반력, F_{thrust,1000 kN}은 충격해석으로부터 1000 kN 프로펠러 굽힘방향 충격력에 대한 주스트러트 베어링에서의 반력 해석결과, d_{measure,bending}은 추력베어링 하우징에서 계측한 굽힘방향 충격 변위, d_{1000 kN,bending}은 충격해석을 통해 추력베어링 하우징에서의 굽힘방향 충격 변위 해석결과이다.

Fig. 7은 충격지속시간 0.01초, 0.02초, 0.05초, 0.1초, 0.2초, 0.3초, 0.5초, 1.0초에 대해 프로펠러에 굽힘방향 하중 10⁶ N 인가 시 주스트러트 베어링 반력 및 추력베어링에서의 굽힘방향 가속도의 진동변위 응답이다.

Fig. 7

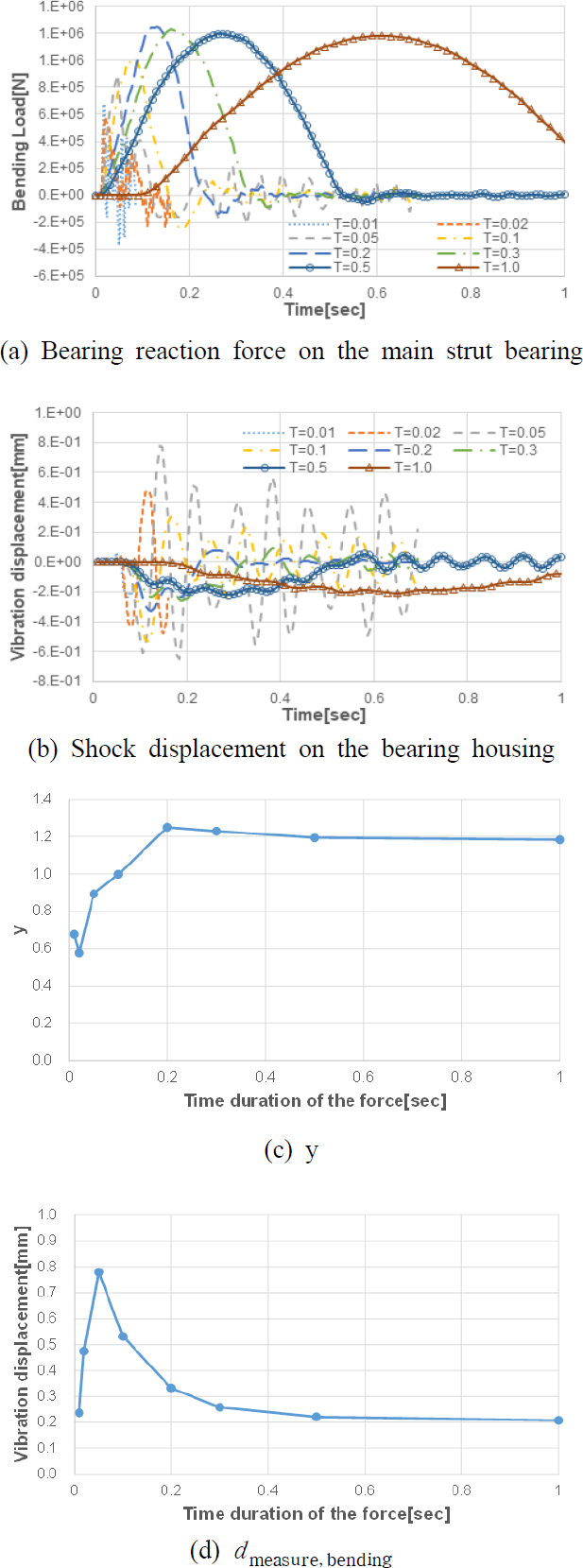
Bearing reaction force on the main strut bearing and shock displacement on the bearing housing for the bending shock

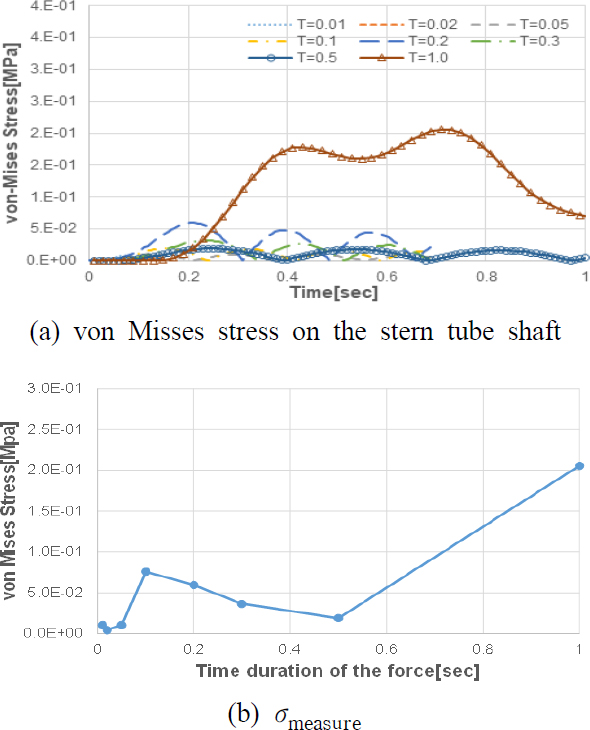
비틀림 방향의 경우 Fig. 8과 같이 스턴튜브 축에서 구한 비틀림 응력과 프로펠러에 입력으로 가한 비틀림 충격력과의 관계를 충격지속시간에 따라 각각 구하였다.

Fig. 8

Shock in the torsional direction and resultant stress on the stern tube shaft

따라서 상태감시시스템으로부터 비틀림 방향 충격 발생 시 충격지속시간과 스턴튜브 축에서의 비틀림 응력을 계측하면 프로펠러에 작용한 비틀림방향 충격력을 식 (5)와 같이 정의할 수 있다.

여기서 T_pp,torsion은 프로펠러 충격 비틀림 토크, σ_measure는 스턴튜브축에서 계측한 비틀림 충격응력, σ_{100 kNm}는 충격해석을 통해 프로펠러에 100 kNm 충격력 입력 시 계산된 스턴튜브축의 비틀림 진동 해석 결과이다.

Fig. 9는 충격지속시간 0.01초, 0.02초, 0.05초, 0.1초, 0.2초, 0.3초, 0.5초, 1.0초에 대해 프로펠러에 비틀림 충격토크 100 kNm 인가 시 스턴튜브축에서의 비틀림 응력에 대한 응답이다.

Fig. 9

von-Misses stress on the stern tube shaft for the torsional shock

이와 같이 충격력 발생 시 각 방향별로 상태감시 센서값을 가지고 프로펠러에 작용한 충격력의 각 방향별 값을 예측할 수 있으며 예측된 프로펠러 인가 충격력을 가지고 추진축계의 디지털 트윈 모델 해석을 수행하면 최대응력 지점 및 크기를 알 수 있으므로 이를 가지고 축의 건전성을 파악할 수 있다.

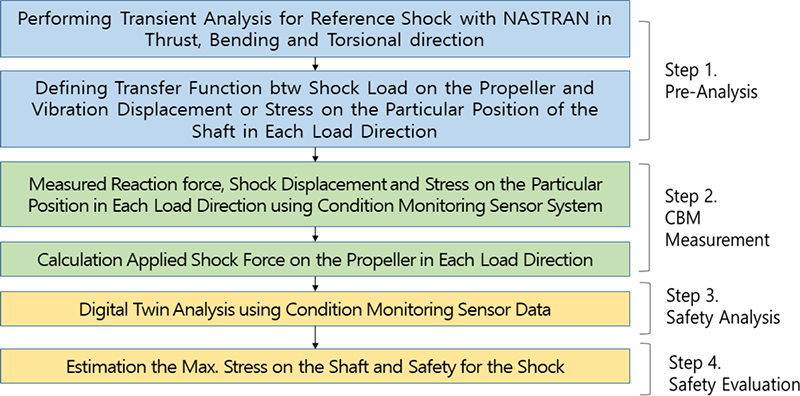
이 절에서 다룬 특정함정의 충격력에 대한 디지털 트윈 해석결과로부터 추진축계 디지털 트윈 모델을 가지고 축의 건전성을 평가하는 절차에 대해 Fig. 10과 같이 제안하고자 한다. Fig. 10과 같이 우선 추진축계에 대한 디지털 트윈 모델을 FEM으로 모델링하고 충격력을 축방향, 굽힘방향 및 비틀림 방향 하중으로 분리한 후 방향별 기준(reference) 하중에 대해 상태감시 센서 설치 위치에서의 응답을 계산한다. 이로부터 프로펠러에 작용하는 충격력과 상태감시시스템에서 계측한 물리량과의 관계를 충격력의 지속시간에 따라 각각 정의할 수 있다.

Fig. 10

Procedure to the shaft safety evaluation using digital twin analysis

다음으로 해석에서 설정한 상태감시 센서를 선정하여 설치위치에 장착 후 함을 운용하고 충격 이벤트 발생 시 상태시스템 센서에서 계측한 물리량을 가지고 프로펠러의 충격력 및 지속시간을 축방향, 굽힘방향 및 비틀림 방향으로 분리하여 정의한다. 굽힘방향 하중은 축중심선에 대해 수직 및 수평방향 교차 축에 대해서 각각 정의할 수 있도록 상태감시 센서를 장착해야만 한다.

이후 정의된 프로펠러 충격력에 대해서 추진축계 디지털 트윈 모델에 인가하여 충격 시 최대응력 발생 위치 및 크기를 구하고 이를 통해 축계 건전성 평가를 수행하도록 구성하였다.

4. 추진축계 건전성 평가 및 수명 예측

4.1 정상상태 수명예측

일반적으로 정상운전상태에서의 추진축계에 가해지는 최대응력과 위치는 시험 및 해석을 통해서 정의할 수 있다.

정상운전상태에서 추진축계는 선형시스템이므로 정상 운전 조건에서 축계에 인가되는 하중이 중가하면 해석 및 시운전 시 식별한 최대 응력 지점에서 하중 변화량 만큼 응력이 증가한다고 가정할 수 있다. 따라서 해석 및 시운전을 통해 최대응력점을 식별하여 선정하고 상태감시시스템을 통해서 해당 위치에서의 하중을 계측하면 최대응력점에서 최대응력이 얼마나 작용하는지 파악할 수 있기 때문에 별도의 디지털 트윈 적용은 불필요하며 상태감시시스템과 고장진단 및 수명예측 알고리즘만 가지고도 CBM+ 구현이 가능하다.

일반적으로 최대응력이 피로한도 이내일 경우 추진축의 수명은 무한한 것으로 가정할 수 있으나 피로한도 이상의 하중이 발생할 경우 Palmgren Miner의 선형손상누적법에 따라 손상도가 1.0 이상이 될 때 파손이 일어난다고 가정할 수 있다⁽⁹⁾.

함정에 사용되는 추진축계의 재질은 강재로 수명곡선은 일반적으로 잘 알려져 있으므로 수명곡선을 가지고 손상도를 구할수 있다.

일반적으로 강재의 수명곡선은 식 (6) ~ 식 (8)과 같이 나타낼 수 있으며 정적 부하에 따라 Goodman 이론을 고려하여 피로한도는 식 (9)와 같이 재산정할 수 있다⁽¹⁰⁾.

이러한 수명곡선을 가지고 피로한도 이상의 하중이 인가되었을 때 축계의 손상도는 식 (10)과 같이 나타낼수 있으며 축계의 잔여수명은 선형손상누적법에 따라 식 (11)과 같이 나타낼 수 있다.

$\[ \begin{array}{l}\mathrm{l}\mathrm{o}\mathrm{g}\left(S\right)=-a\mathrm{l}\mathrm{o}\mathrm{g}\left(N\right)+b\\ =-a\mathrm{l}\mathrm{o}\mathrm{g}\left(N\right) +\mathrm{l}\mathrm{o}\mathrm{g}\left(B\right), S=B\times N^{-a}\end{array} \]$

(6)

$\[ a=\frac{1}{3}\mathrm{l}\mathrm{o}\mathrm{g}\left({\sigma }_Y\right)-\mathrm{l}\mathrm{o}\mathrm{g}\left({\sigma }_F^{\text{'}}\right) \]$

(7)

$\[ B={10}^{\left(3a+\mathrm{l}\mathrm{o}\mathrm{g}\left({\sigma }_Y\right)\right)} \]$

(8)

$\[ {\sigma }_F^{\text{'}}=\left(1-\frac{{\sigma }_s}{{\sigma }_Y}\right)\cdot {\sigma }_F \]$

(9)

$\[ D=\sum _{i=1}^n \frac{N_i}{N_{f,i}} \]$

(10)

$\[ \mathrm{R}\mathrm{U}\mathrm{N}\left[\%\right]=\left(1-D\right)\times 100\% \]$

(11)

여기서 S는 응력, N은 수명, α, B는 수명곡선의 기울기 및 Y 절편, σ_Y는 인장강도, σ_F는 정하중이 없을 때 피로한도, $$ {\sigma }_F^{\text{'}}$$은 정하중이 작용했을대 피로한도, σ_S는 정적응력, D는 손상도, N_i는 피로한도 이상의 부하 가진 횟수, N_f,i는 피로한도 이상 하중 인가 시 해당 하중에 대한 피로수명, D_∆t는 ∆t 시간 동안 받은 손상도, RUN [%]는 전체수명에 대한 잔여수명률이다.

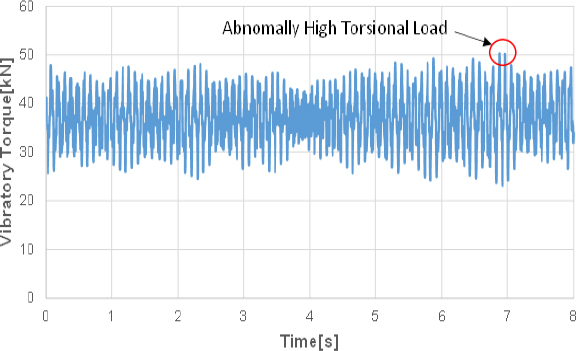
Fig. 11은 특정함정 최대속도에서의 8초 동안 계측한 비틀림 진동 토크이며 이는 최대응력을 가지는 축의 비틀림 진동응력을 계측하기 위해 설치된 스트레인게이지 및 텔리메트리로부터 계측한 진동 응력이다. 이 경우 정상운전상태에서 축방항응력 및 굽힘응력은 무시할 수 있으므로 최대 응력은 비틀림 응력만 고려하여 축의 수명을 평가하였다. Fig. 11에서 피로한도를 초과하는 이벤트는 8초 중 1회 발생하였으며, 이를 붉은 원으로 표기해 놓았다.

Fig. 11

Tosional vibratory torque for a particular ship when sailing

Fig. 11의 데이터를 가지고 레인플로어 싸이클 카운팅(rain flow cylce counting) 방법을 이용하여 변동응력에 대한 정적응력을 산정하고 이를 이용하여 각각의 변동응력에 대해 손상도를 식 (6) ~ 식 (10)을 이용하여 계산해서 수명을 예측해 보았다. 수명예측 결과 Table 3과 같이 Fig. 11의 이벤트(8초)가 10시간 반복하여 인가되었을 경우 수명은 약 0.5 % 감소됨을 알 수 있었다.

Table 3

Estimating results of the life cycle of the propulsion shaft under Fig. 10 conditions

이와 같이 정상상태 운전 조건에서는 운전 속도 별 최대응력 지점을 알 수 있고 상태감시시스템을 통해 해당 응력 계측이 가능하기 때문에 상태감시시스템만으로 추진축계의 건전성 평가 및 수명예측이 가능함을 알 수 있었다.

4.2 비정상상태 수명예측

충돌과 같은 비정상상태 운전조건의 경우 충돌의 방향, 충격력의 지속시간이 확정적이지 않기 때문에 충돌의 상태에 따라 최대응력 지점이 달라지고 응력의 크기도 달라진다. 따라서 실선 시운전이나 해석을 통해 모든 충돌상황을 고려해서 축계의 건전성을 평가하는 것은 불가능하다.

따라서 2절에서 기술한 바와 같이 충돌 시 충격력을 축방향 스러스트 하중, 축 중심선 수직 및 수평 교차 방향 굽힘하중, 축 회전방향 비틀림 토크로 구분하고 각 방향의 하중을 계측할 수 있는 상태감시시스템을 장착하는 것을 제안하였다. 따라서 각 분력을 계측하여 충돌 시 충격력을 정의하고 이를 입력으로 디지털 트윈 모델을 가지고 충격해석을 수행하여 최대응력 발생 위치 및 크기를 계산하고 이를 통해 축의 건전성 및 수명을 예측하는 방법을 제안하였다.

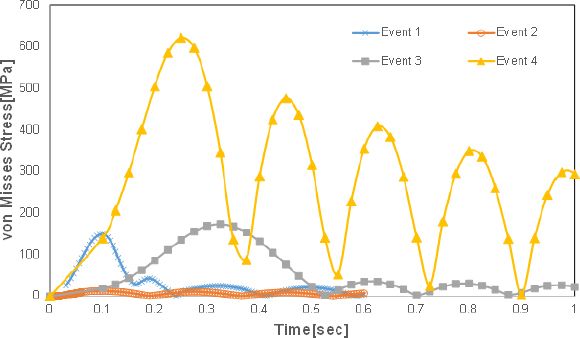
이 절에서는 2절에서 다룬 추진축계 모델에 대해 Table 4와 같이 4가지 충돌상황을 가정하고 각 방향별 충돌하중을 이론적으로 계산하여 상태감시시스템으로부터 계측한 것으로 가정한 후 충격해석을 수행하였다.

Table 4

Applied load to the propeller for event 1 ~ 4

Table 4에서 이벤트 1은 프로펠러가 200 r/min으로 회전하고 있는 조건에서 프로펠러가 해저에 접촉하여 충돌에 의한 추력, 굽힘하중 및 비틀림 토크가 발생한 것으로 가정하였다.

여기서 각 방향별 충격 하중은 프로펠러 충돌에 대한 선급규칙으로 극 지방을 운항하는 선박의 프로펠러가 얼음에 부딪칠 때 충격력에 대한 기준(ship for navigation in ice, DNVGL)을 도입하여 충격력을 계산하였다.

이때 정격 토크와 추력은 함 설계 기준에 따라 해당 속도에서의 토크 및 추력을 사용하였다. 충격시간은 200 r/min 회전 중 프로펠러의 90° 간격 동안 충격이 발생한 것으로 가정하여 1회전의 1/4 시간인 0.075초에 발생한 것으로 가정하였다.

이벤트 2는 수면근처 수중에 정지해 있는 200 kg 통나무를 함정이 최대속도 회전수인 220 r/min 속도에서 프로펠러와 충돌하는 상황으로 가정하였다. 이때 충격력은 반경방향의 굽힘하중과 접선방향 하중에 의한 비틀림 토크로 정의하였다. 이때의 충격 굽힘하중은 충돌지속시간을 0.03초로 가정하여 식 (12)의 충돌 에너지식을 통해 계산하였고, 접선하중은 굽힘하중과 동일하다고 가정하여 접선하중에 반경을 곱하여 계산하였다.

통나무는 정지해 있다가 충돌 시 함속과 동일한 속도로 움직이는 것으로 가정하였다.

$\[ m{v}_2-m{v}_1=\int Fdt=F\Delta t \]$

(12)

여기서 m은 충돌하는 통나무의 질량, v₁, v₂는 충돌 전, 후 통나무의 속도, F는 충돌 시 충격력, ∆t는 충돌지속시간이다.

이벤트 3 ~ 이벤트 4의 경우 프로펠러가 120 r/min 및 220 r/min으로 회전하고 있는 조건에서 어망이 감기는 상황으로 충격력은 어망 감김으로 인한 비틀림 토크로 가정하고 충격 시간은 120 r/min 및 200 r/min 1회전수 동안 어망이 감긴다고 가정하여 충격지속시간을 0.5초 및 0.3초로 각각 가정하였다.

이때 비틀림 충격하중은 식 (13)의 충돌 에너지식을 이용하여 계산하였다. 식 (13)에서 프로펠러는 어망감김으로 인해 정지하는 것으로 가정하였다.

$\[ I{\omega }_2-I{\omega }_1=\int Qdt=Q\Delta t \]$

(13)

여기서 I는 프로펠러의 질량관성 모멘트, ω₁, ω₂는 프로펠러 어망감김 전, 후 프로펠러의 회전 각속도(=2πn₁/60, 2πn₂/60), n₁, n₂는 프로펠러 어망감김 전, 후 축회전수, Q는 어망감김으로 발생한 프로펠러의 비틀림 충격 토크, ∆t는 충격지속시간이다.

비정상 충격 하중에 대한 해석은 우선 정격토크, 정격추력 및 자중에 의한 굽힘하중을 적용하여 선형정적해석을 Nastran 101번 해석 방법을 이용하여 수행하고, 충격하중의 경우 정하중은 고려하지 않고 비틀림 충격토크, 충격 추력 및 충격 굽힘 하중을 적용하여 모달(modal) 방법을 이용한 트랜지언트(transient) 해석을 Nastran 112번 해석방법을 통해서 수행하였다. 이후 해석에서 얻어진 정적응력과 충격응력을 가지고 전절의 식 (6) ~ 식 (10)을 통해 잔여수명을 계산하였다.

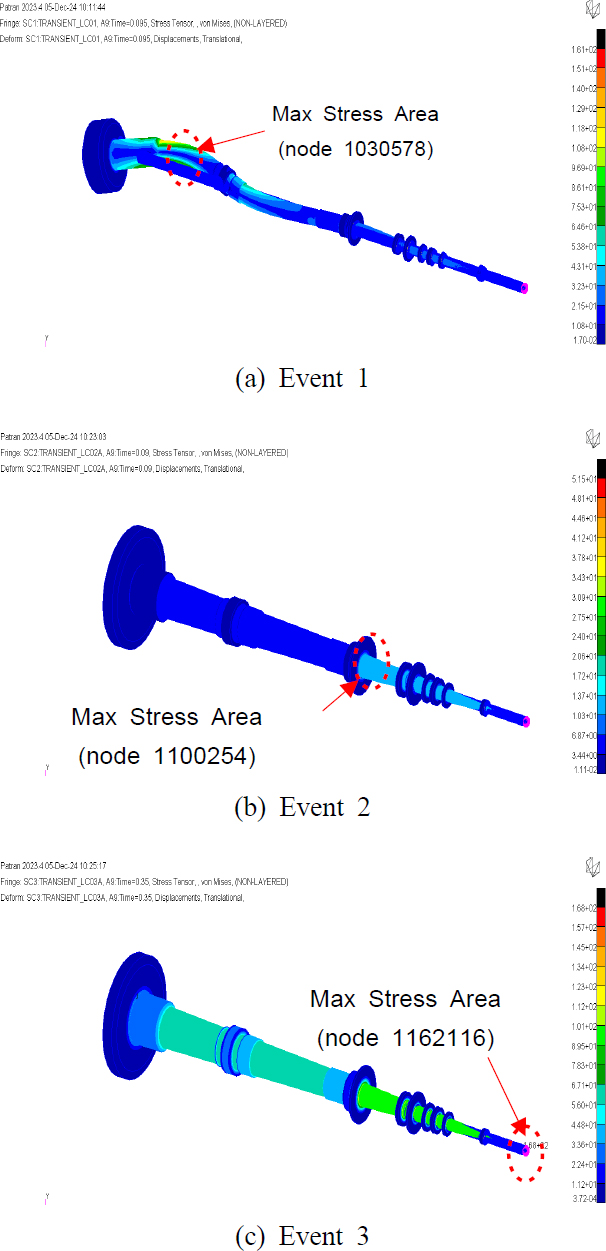
Fig. 12와 Fig. 13은 Table 4의 각 하중조건에 대한 최대응력점 위치 및 최대응력의 시간 이력을 보여주고 있다. Fig. 12에서 충격 이벤트는 충격 이후 가장 큰 응력점만 고려하여 손상도를 산출하였다.

Fig. 12

Stress distribution under the shock event

Fig. 13

Time history of the max. stress resulted by transient analysis for event 1 ~ 4

Table 5는 이벤트 1 ~ 이벤트 4 충격하중에 따른 축의 최대응력점에서의 응력값을 기준으로 충격 발생 후 잔여수명을 계산한 결과이다. 여기서 진여수명은 충격이 10³번 반복되었을 때를 기준으로 산정하였다. 피로한도의 경우 정하중이 없을 때 순수 변동하중에 따른 피로한도와 정적해석을 통해 얻어진 정적최대응력을 기준으로 식 (8)에 따라 수정된 피로한도를 같이 명기하였다.

Table 5

RUL estimation results under event 1 ~ 4

이벤트 1의 경우 최대 충격응력값이 피로한도의 약 87 %로 축의 건전성에 거의 영향이 없음을 알 수 있었다. 이벤트 2의 경우도 최대 충격응력값이 피로한도보다 충분히 작아 축의 건전성에는 영향이 없음을 알 수 있었다.

하지만 이벤트 3의 경우 최대 충격응력이 피로한도 보다 높아 손상도가 발생하며 10³번 충격을 가정했을 때 선형손상누적법에 의해 약 0.1 % 수명이 줄어듦을 알 수 있었으며 9.6×10⁵번 반복 충격 시 파손이 일어난다고 볼 수 있으므로 큰 손상을 야기 시키는 이벤트는 아닌 것으로 파악할 수 있었다. 고속조건에서 프로펠러에 어망이 감기는 이벤트인 이벤트 4의 경우 인장강도에 근접한 충격하중이 발생함을 예측할 수 있었으며 이러한 이벤트가 691번 반복 될 경우 파손이 일어나는 것으로 해석되었다. 하지만 이 경우 1번 충격 이벤트 발생 시 이미 항복강도를 초과하는 응력이 발생됨에 따라 1번의 충격만으로도 추진축계에 큰 손상을 야기할수 있으므로 바로 정비가 필요한 이벤트이다.

따라서 이벤트 1 ~ 이벤트 4에 대한 추진축계 디지털 트윈 모델 해석결과로부터 디지털 트윈 모델을 통한 축의 건전성 평가가 가능함을 파악할 수 있었다. 또한 가상이벤트에 대한 추진축계 디지털 트윈 모델 해석 결과로부터 프로펠러에 로프가 감겨 비틀림 방향으로 충격토크가 발생하는 이벤트 3 ~ 이벤트 4가 가장 큰 손상도를 유발함을 알 수 있었다.

5. 추진축계 디지털 트윈 모델을 이용한 축계의 상태기반예지정비(CBM+) 알고리즘

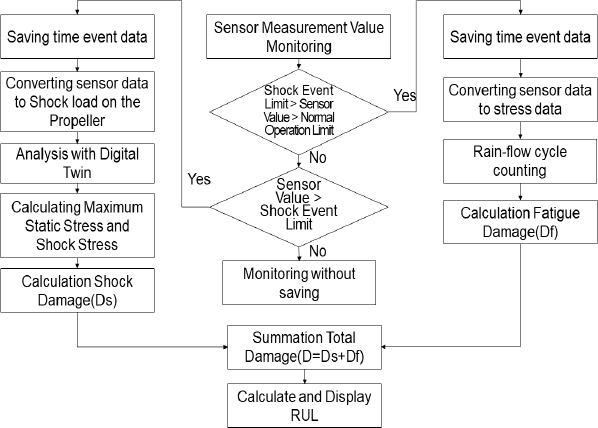
이 연구에서는 앞절의 검토결과를 바탕으로 추진축계 디지털 트윈 모델에 대해 함정에 장착되어 있는 상태감시시스템의 값을 입력으로 한 디지털 트윈 해석을 통해 축계의 건전성 평가 및 수명예측 알고리즘을 다음과 같이 제안하고자 한다. 알고리즘은 Fig. 14와 같이 축 건전성 및 수명예측을 위한 상태감시시스템으로부터 데이터를 1초 간격으로 계측하고 정상운전조건에서 기준치 이상의 과도 하중 발생 시 상태감시데이터를 가지고 축계 최대응력값으로 산정한 다음 레인플로어 싸이클 카운팅(rain-flow cycle counting) 기법을 적용하여 피로손상도를 계산한다. 만약 과도하중이 충격 하중 기준치 이상일 경우 기존에 정의된 상태감시센서 데이터와 프로펠러 하중간 관계를 통해 프로펠러에 가해진 충격하중을 정의하고 이를 입력으로 하는 디지털 트윈 모델 해석을 수행하며, 그 결과로부터 얻어진 최대응력을 가지고 충격하중에 의한 충격손상도를 계산한다. 축계가 받는 총 손상도는 정상하중 조건에서의 피로손상도와 충격하중 조건에서의 충격손상도를 합친 값이며 이 값을 가지고 식 (10)으로부터 축계의 잔여수명을 계산하여 전시하도록 구성하였다. 총 누적 손상도가 1.0일 경우 고장이 발생하므로 정비 시기는 손상도가 1.0이 되기 전 충분한 기간을 두고 설정하는 것이 타당할 것으로 판단된다.

Fig. 14

Flow chart for calculating total damage and RUL

6. 결 론

함정의 경우 매우 험한 환경 아래에서 운용되고 있기 때문에 정상운전 조건에서 함의 부하증가 및 가진력 증가에 의해 주요 장비 및 체계에 피로에 의한 고장이 발생할 수 있다. 또한 수중 부유물과의 충돌, 프로펠러의 어망 감김, 암초 등과의 충돌 등 비정상적 이벤트도 종종 발생되며 이로인해 추진축에 대한 고장 및 파손 문제가 빈번히 발생되고 있다. 추진축 관련하여 정상운전 조건의 경우 부하증가에 따른 추진축의 피로 손상도는 상태감시시스템으로 계측한 진동, 응력 신호 등을 가지고 바로 예측이 가능하나 충돌과 같은 비정상적 이벤트가 발생할 경우 이러한 이벤트로 인한 추진축계의 건전성 및 손상도를 정확히 알 수 없으므로 함정 자체적으로 정비여부를 판단하기가 매우 어려운 상황이다.

이 연구에서는 이러한 충격 이벤트에 대한 추진축계 건전성 및 수명 예측을 위해 충격력을 정의할 수 있는 상태감시시스템 및 디지털 트윈의 적용을 제안하였으며 가상 이벤트에 대한 디지털 트윈 모델 해석을 통해 추진축계의 건전성 및 잔여수명을 예측하는 절차를 제안하였다. 이 연구에서 제안한 방법을 적용할 경우 정상적인 운전조건 뿐만아니라 비정상적 과도 이벤트에 대한 축계 손상도를 모두 고려하여 추진축계의 정비여부를 결정할 수 있으며 잔여수명에 대한 예측도 가능하므로 적기에 함정 정비를 수행하고 정비 자재 준비가 가능해져 군의 전력 공백을 최소화 할 수 있을 것으로 기대된다.

이 연구를 기반으로 향후 실제 상태시스템과 연계하여 추진축계의 디지털 트윈의 검증 및 평가를 수행할 예정이다. 적용함정이 정해지면 이 연구의 결과를 활용하여 가장 효과적으로 디지털 트윈의 가진력을 결정할 수 있는 센서의 종류, 위치 선정에 대한 검토가 필요하며 센서 입력값에 대한 노이즈 방지 대책도 필요하다.

현재 국내 해군의 경우 군위성 등 함정의 센서데이터를 실시간으로 전송받아 처리하기 힘들기 때문에 함정 입항 시 이벤트 데이터를 육상 서버에 업로딩하고 각 이벤트 데이터를 가지고 디지털 트윈 해석을 통해 추진축게의 손상도를 파악하는 방식의 디지털 트윈부터 적용할 예정이다.

References

• Oh, S., Park, D., Baek, H., Kim, S., Lee, J.-K. and Kim, J.-G., 2020, Virtual Sensing System of Structural Vibration using Digital Twin, Transactions of the Korean Society for Noise and Vibration Engineering, Vol. 30, No. 2, pp. 149~160. [https://doi.org/10.5050/KSNVE.2020.30.2.149]
• Hwang, S.-B., Jeong, S.-J. and Yoon, S.-W., 2020, The Design of Manufacturing Simulation Modeling based on Digital Twin Concept, Journal of the Korea Society for Simulation, Vol. 29, No. 2, pp. 11~20.
• Heron, J. W., Forster, A., Milne, R., Milne, D. and Allen, R., 2022, Digital Twin for In-line Fault Prediction in Military Unmanned Vehicles, Science & Technology Organization, Brussels, Belgium.
• Lee, J.-H., Nam, Y.-S., Kim, Y., Liu, Y., Lee, J. and Yang, H., 2022, Real-time Digital Twin for Ship Operation in Waves, Ocean Engineering, Vol. 266, 112867. [https://doi.org/10.1016/j.oceaneng.2022.112867]
• Fonseca, Í. A., Gaspar, H. M., de Mello, P. C. and Sasaki, H. A. U., 2022, A Standards-based Digital Twin of an Experiment with a Scale Model Ship, Computer-aided Design, Vol. 145, 103191. [https://doi.org/10.1016/j.cad.2021.103191]
• Oh, S., Lee, K.-H., Ahn, K., Yu, Y., Kim, K. and Kim, J.-G., 2021, Development of Vibro-acoustic Virtual Sensing System for Pipeline Structure using Digital Twin, Transactions of the Korean Society of Mechanical Engineers A, Vol. 45, No. 9, pp. 805~815. [https://doi.org/10.3795/KSME-A.2021.45.9.805]
• Park, G., Cho, Y., Oh, S., Lee, J., Park, S. et al., 2024, Virtual Sensing System of Vehicle Steering Motor with Virtual Reality, Transactions of the Korean Society for Noise and Vibration Engineering, Vol. 34, No. 1, pp. 33~41. [https://doi.org/10.5050/KSNVE.2024.34.1.033]
• Borkowski, M., 2017, NAVSEA’s Condition Based Maintenance Plus(CBM+) Initiative, NAVSEA(naval sea systems command), DC, United States.
• Miner, M. A., 1945, Cumulative Damage in Fatigue, Journal of Applied Mechanics, Vol. 12, No. 3, pp. A159~A164. [https://doi.org/10.1115/1.4009458]
• Budynas, R. G. and Nisbett, J. K., 2011, Shigley’s Mechanical Engineering Design, 9th Edition, McGraw-Hill, NY, United States.